Capítulo 4 - MÉTODO
DE INSPEÇÃO POR CORRENTES PARASITAS
traduzido do livro: AIR
FORCE TO 33B-1-1 / ARMY TM 1-1500-335-23 / NAVY (NAVAIR) 01-1A-16-1 -
Manual Técnico - Métodos de Inspeção Não Destrutiva, Teoria Básica
- PRINCÍPIOS E TEORIA DA INSPEÇÃO POR
CORRENTES
PARASITAS
- Indução das Correntes Parasitas
- Campo Magnético Primário
- Campo Magnético Secundário
- Profundidade de Penetração
- Profundidade Padrão de Penetração
- Profundidade de Penetração
Efetiva
- Temperatura e Profundidade de
Penetração
- Impedância
- Detectabilidade (Sensibilidade)
- Resolução
- Medição da Resistividade
- Medição da Condutividade
- Condutividade com Base no
Percentual do
Padrão de Cobre Recozido Puro (IACS)
- Visão Geral do Sinal de Detecção,
Processamento e Mostradores
- Fontes Geradoras de Sinais
- Sinais de Detecção de Mudanças
de
Propriedades Eletromagnéticas
- Análise dos Sinais
- Mostradores (Telas de
Apresentação) de
Sinais
- Mostradores de
Intensidade/Amplitude do
Sinal
- Mostradores Planos
(Cartesianos ou
Polares)
- Mudanças da Impedância
- Indutância de uma Bobina
- Reatância Indutiva
- Combinação de Quantidades Fora
de Fase
- Representação por Plotagem
X-Y
- Representação no Plano de
Impedãncia
- Diagramas de Impedância
- Objetivo dos Diagramas de
Impedância
- Desenvolvimento de Um Diagrama
de
Impedância
- Típicos Usos de um Diagrama de
Impedância
- Curva de Condutividade
- Variações de Espessura
- Camadas Condutoras
- Normalização da Impedância
- Análises no Plano de Impedância
- Detecção por Fase
- Trincas, Lift-off e
Condutividade
- Detecção de Trincas em
Materiais Não
Ferromagnéticos
- Defasagem com a Profundidade
- Efeitos da Condição de Inspeção no
Ensaio
de Correntes Parasitas
- Frequência do Ensaio
- Condutividade e Frequência
- Acoplamento Eletromagnético
- Fill-Factor
- Corrente Elétrica na Bobina
- Temperatura
- Geometria
- Lift-off
3 PRINCÍPIOS E TEORIA DA INSPEÇÃO DE
CORRENTES PARASITAS
3.1 Indução de Correntes parasitas.
À medida que o campo
eletromagnético de uma bobina penetra em um material condutor, sob a
ação desse campo, ele gera
correntes parasitas paralelas à superfície da peça e em ângulos retos à
direção do campo aplicado (Figura 1). A frequência do fluxo de
correntes parasitas é a mesma do campo eletromagnético.
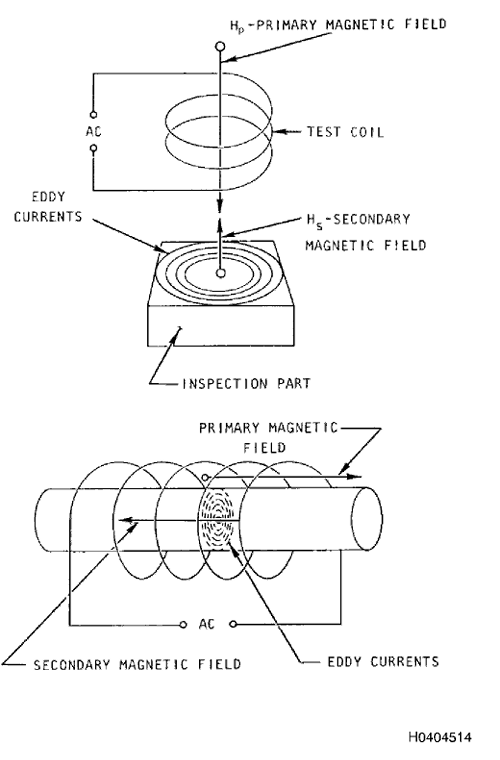
Figura 3.1. Campos Magnéticos Primários e Secundários em ET
3.2 Campo
Eletromagnético Primário.
O campo eletromagnético primário é o campo
magnético da bobina (Figura 1). Este campo é chamado eletromagnético
porque o campo magnético é produzido a partir de eletricidade e não de
um ímã permanente. A taxa na qual o campo eletromagnético varia é
chamada de frequência. A intensidade do campo eletromagnético na
superfície do condutor depende do tamanho e da configuração da bobina,
da quantidade de corrente que circula através da bobina e da distância
da bobina à
superfície. A quantidade de correntes parasitas que o campo primário é
capaz de gerar depende das propriedades da peça ensaiada e da
intensidade do campo eletromagnético secundário que se opõe ao campo
primário.
3.3 Campo Eletromagnético Secundário.
Correntes parasitas
também geram um campo eletromagnético na peça. Este campo, chamado de
campo eletromagnético secundário, se opõe ao campo eletromagnético
primário (Figura 1) e é uma consequência da Lei de Lenz. A Lei de Lenz,
conforme aplicada a este caso, afirma que correntes induzidas
(correntes parasitas) atuam para reduzir a intensidade da corrente
indutora. A oposição do campo secundário ao campo primário diminui a
intensidade geral do campo eletromagnético e reduz tanto a corrente que
flui através da bobina quanto as correntes parasitas resultantes.
Mudanças nas propriedades do material sob inspeção produzem mudanças
nas
correntes parasitas e, portanto, em seus campos magnéticos secundários.
Desta forma, mudanças na peça sob inspeção produzem efeitos que podem
ser detectados monitorando a fonte do campo eletromagnético primário ou
o campo eletromagnético geral.
3.4 Profundidade de Penetração.
A
intensidade das correntes parasitas diminui exponencialmente com a
profundidade em um material. A intensidade em qualquer profundidade é
afetada pelas mesmas variáveis que influenciam a intensidade
superficial das correntes parasitas, embora nem sempre da mesma maneira
ou na mesma quantidade. Em outras palavras, a profundidade de
penetração de uma intensidade específica de correntes parasitas é
afetada pelas variáveis, conforme indicado na Seção 8, Tabela 3.
Geralmente, qualquer parâmetro que aumente a profundidade de
penetração aumentaria a detectabilidade de descontinuidades mais
profundas na peça.
3.4.1 Profundidade Padrão de
Penetração.
Três dessas
variáveis (condutividade, permeabilidade magnética relativa e
frequência) são usadas para definir a profundidade padrão de
penetração. A profundidade padrão de penetração é a profundidade abaixo
da superfície do artigo de inspeção na qual a intensidade do campo
magnético,ou a intensidade das correntes parasitas induzidas, é
reduzida para 36,8% do valor na superfície. A profundidade de
penetração padrão é expressa pela seguinte fórmula no Seção 8,
Parágrafo 8.7.
Como a profundidade de penetração está relacionada apenas a uma
porcentagem da intensidade do campo de superfície (intensidade das
correntes parasitas), algumas variáveis de teste não são incluídas na
fórmula. A configuração, o tamanho, a corrente e o acoplamento
magnético da bobina não são considerados nesta fórmula. Essas variáveis
afetam a magnitude absoluta das correntes parasitas em uma
profundidade especificada, mas não a profundidade de penetração padrão.
Os valores de profundidade de penetração padrão para frequências
selecionadas para várias ligas, ligas de alumínio puro e ligas de
alumínio revestido são mostrados na Seção 8, Tabela 5 e na Tabela 6.
3.4.2 Profundidade de Penetração
Efetiva.
A profundidade
de penetração efetiva é a profundidade na peça inspecionada na qual a
intensidade do campo magnético ou a intensidade das correntes parasitas
induzidas é reduzida para 5% do valor na superfície. Esta profundidade
é aproximadamente 3 vezes a profundidade padrão de penetração (de
acordo com ASTM E1004, a profundidade efetiva de penetração usada para
fins de medição de condutividade é 2,6). A profundidade efetiva de
penetração é usada para determinar a frequência do ensaio ao trabalhar
com materiais finos, de modo que o campo eletromagnético geral não se
estenda além da superfície traseira da peça ensaiada, de modo que os
efeitos de variação da espessura possam ser suprimidos. A espessura
mínima do material necessária para medição de condutividade de várias
ligas a 60 kHz e 480 kHz usando os valores ASTM de 2,6 é mostrada na
Seção 8, Tabela 3.
3.4.3 Temperatura e Profundidade de
Penetração.
Para a maioria das aplicações, a
temperatura não é um fator
importante na determinação da profundidade de penetração. No entanto,
se necessário, os efeitos da temperatura seriam incluídos como ajustes
aos valores de condutividade e permeabilidade magnética relativa usados
na fórmula para calcular a profundidade padrão de penetração.
3.5
Impedância.
Impedância é a oposição total ao fluxo de corrente
representada pelo efeito combinado de resistência, indutância e
capacitância de um circuito.
3.6 Detectabilidade/Sensibilidade.
A capacidade de um
instrumento de correntes parasitas de detectar pequenas variações na
impedância da bobina de ensaio é uma medida de sua detectabilidae. Essa
qualidade está inter-relacionada com as propriedades da bobina de
ensaio
e a frequência de operação. Portanto, a sensibilidade do instrumento a
uma condição de falha específica ou propriedade do material DEVE ser
estabelecida a partir de padrões de referência que representem essa
condição.
3.7 Resolução.
A capacidade de um sistema de ensaio separar
os sinais de duas indicações próximas é definida como resolução. Essa
propriedade, mais a detectabilidade/sensibilidade, deve ser considerada
em todas as
situações de avaliação de falhas. O projeto da sonda, a frequência
do ensaio e o projeto da instrumentação são fatores determinantes
da
resolução de um sistema de correntes parasitas.
3.8 Medição de
Resistividade.
Resistência elétrica é uma medida da resistência ao fluxo
de corrente elétrica em um condutor. A resistência depende do
comprimento e da área do caminho da corrente e da condutividade do
condutor. A resistência é comumente medida em ohms. Se um material
permite que um volt (potencial elétrico) de força motriz empurre um
ampère de corrente através de um condutor, a resistência elétrica do
condutor é definida como um ohm de resistência. Resistividade é um
parâmetro material independente do tamanho de uma amostra de material e
está relacionada à resistência. Resistividade é definida como ohms
vezes área da seção transversal dividida por unidade de comprimento
(Seção 8, Parágrafo 8.1.3). (NT: Resistência é uma característica do
condutor,
enquanto a Resistividade é uma propriedade do material constituinte do
condutor)
3.9 Medição de Condutividade.
Condutividade elétrica
é o recíproco (inverso) da resistividade elétrica. O recíproco do ohm
(resistência) é comumente
chamado de mho (condutância). A condutividade é comumente expressa em
unidades de mho
por unidade de comprimento; como mho/polegada ou mho/metro. As relações
entre condutividade, resistividade e resistência são expressas pelas
equações na Seção 8, Parágrafo 8.12.
3.9.1 Condutividade Baseada na
Porcentagem
do Padrão Internacional de Cobre Recozido Puro (%IACS).
Uma forma
alternativa de expressar a condutividade é uma porcentagem da
condutividade de um material conhecido. A Comissão Eletrotécnica
Internacional designou a condutividade de um grau específico de cobre
de alta pureza como o padrão para este método alternativo, com uma
condutividade de 100%. É chamado de Padrão Internacional de Cobre
Recozido Puro (IACS). A condutividade de todos os outros metais é então
expressa como uma porcentagem deste padrão.
NOTA:
Os valores de
condutividade de alguns materiais de engenharia comumente usados
estão listados na Tabela 2 e na Tabela 7 na Seçãoo 8. A
porcentagem IACS é a forma usual de expressar a condutividade em END
aeroespacial.
3.10 Visão Geral da Detecção, Processamento e Exibição de
Sinais.
3.10.1 Fontes de Sinal.
Ao executar uma técnica de correntes
parasitas, as alterações no material podem ser detectadas monitorando a
corrente alternada na bobina (arranjo de bobina única) ou usando uma
bobina sensora separada para monitorar o campo eletromagnético
resultante. Esses sinais podem ser analisados para obter informações
relevantes à inspeção que está sendo conduzida. O importante a ser
observado é que a bobina que está atuando como receptor está produzindo
uma corrente elétrica que está adiantada ou atrasada em relação à
corrente do oscilador do instrumento. A diferença entre essa
antecipação ou atraso é o ângulo de fase.
3.10.2 Detecção de Sinal.
Uma
técnica simples, porém eficaz, de detecção de sinal é usar um circuito
em ponte, como ilustrado na Figura 2. Com a corrente fluindo pela
bobina de ensaio e a bobina posicionada em uma área sem falhas ou de
referência, a impedância variável Z1 pode ser ajustada para que a
corrente zero flua pelo amplificador. Esse ajuste é denominado
balanceamento ou anulação da ponte. Quando a bobina é colocada em uma
área com falhas ou danificada, a mudança resultante na corrente através
da bobina "desequilibra" a ponte e a corrente flui pelo
amplificador.Esta corrente é o sinal de inspeção. O sinal tem a mesma
frequência que a corrente através da bobina. A fase e a amplitude deste
sinal contêm informações sobre a condição que causou o desequilíbrio da
ponte.
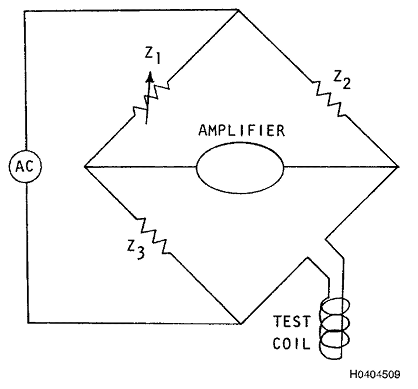
Figura 3.2. Circuito de Ponte Simplificado
3.10.3 Análise de
Sinal.
No tipo mais simples de
instrumentação, a análise do sinal
consiste em medir a mudança na amplitude/magnitude/intensidade da
corrente que flui através
da ponte. Mudanças na intensidade da corrente alternada são
amplificadas
e convertidas em corrente contínua para exibição ou leitura. Em
instrumentação mais sofisticada, tanto a amplitude quanto a fase são
medidas.
3.10.4 Mostrador/Tela ("Displays").
O método pelo qual os sinais de
correntes
parasitas são apresentados é ditado pelo tipo de informação necessária
e pela complexidade da instrumentação. Quando apenas a amplitude do
sinal é medida, medidores, sinais de alarme ou registradores são
comumente usados. Quando as informações de amplitude e fase devem ser
exibidas, um dispositivo de exibição bidimensional (NT: Tipicamente uma
Tela Analógica [passado], Digital [atualmente], ou mesmo um monitor
eletrêonico ou de um notebook) )é normalmente usado.
3.10.4.1 Monitores/mostradores de
Amplitude.
Os medidores podem ser analógicos
(agulha movendo-se sobre uma escala numérica fixa) ou digitais
(números). Alarmes
sonoros ou visuais podem ser configurados para disparar quando a
amplitude do sinal excede um limite predeterminado. Um registrador
apresenta um registro contínuo da amplitude do sinal durante uma
inspeção para análise subsequente.
3.10.4.2 Exibição do Plano de
Impedância (Gráfico de Lissajous, Gráfico Cartesiano ou Polar).
Defeitos ou outras variações nas
características do
material alterarão a intensidade e a distribuição de um fluxo de
corrente parasita induzido. Alterações no fluxo de corrente parasita
resultarão em alterações nas correntes da bobina indutora ou da bobina
do sensor. Essas alterações podem ser expressas como uma alteração
aparente na impedância elétrica da bobina. Isso torna possível associar
alterações nas propriedades do material a alterações específicas na
impedância aparente das bobinas de excitação ou do sensor. A exibição
bidimensional que permite isso é a mais comumente usada e é chamada de
exibição do plano de impedância. O plano de impedância é discutido mais
detalhadamente na Seção 4, Parágrafo 3.10.8.2.
3.10.5 Alterações na
Impedância.
A impedância de uma bobina parece
mudar quando ela é
colocada adjacente a uma parte eletricamente condutiva ou
ferromagnética. O campo eletromagnético secundário criado pela corrente
parasita induzida na peça se opõe ao campo primário. Este campo oposto
também induz um fluxo de corrente na bobina em oposição à corrente
primária. Se a peça não for ferromagnética, o campo magnético líquido
resultante da combinação dos campos primário e secundário diminui em
magnitude, assim como o fluxo de corrente na bobina. Isso equivale a
diminuir a indutância e aumentar a resistência da bobina. Se a peça for
ferromagnética, o campo magnético líquido aumenta devido ao efeito de
ampliação da permeabilidade magnética relativa, mas o fluxo de corrente
na bobina diminui devido ao efeito oposto do campo magnético secundário
das correntes parasitas induzidas.Isto é equivalente a aumentar tanto a
indutância quanto a resistência da bobina. Desta forma, mudanças em uma
peça que afetam a intensidade do campo magnético na superfície da peça
ou a intensidade e distribuição das correntes parasitas na peça, mudam
a impedância aparente da(s) bobina(s) de ensaio. Estas variações no
fluxo de corrente, tanto de fase quanto de amplitude, podem ser
detectadas, amplificadas, exibidas e analisadas como resultados de
ensaios de correntes parasitas. As mudanças de amplitude e fase nos
sinais podem ser relacionadas a mudanças nas peças inspecionadas.
3.10.6 Indutância de uma bobina.
A indutância de uma bobina depende do
número de voltas na bobina, do tamanho da bobina, da permeabilidade do
material dentro da bobina (por exemplo, o núcleo da bobina) e do fluxo
magnético total através da bobina. Um método alternativo de expressar
auto-indutância (L) é
L = n . Φ / I
Onde:
L = Indutância
(henry)
n = Número de voltas na bobina
Φ = Fluxo magnético
(Weber)
I = Corrente através da bobina
(Ampere)
3.10.7 Reatância
indutiva.
A medida da quantidade de oposição ou
resistência (ohm) ao
fluxo de corrente alternada devido à indutância em uma bobina é chamada
de reatância indutiva. A reatância indutiva depende do valor da
indutância da bobina e da frequência da corrente alternada. A reatância
indutiva aumenta à medida que a indutância ou a frequência aumentam.
Isso pode ser expresso pela seguinte equação:
XL = 2 . π . f . L
Onde:
XL = Reatância
indutiva (ohm)
π = 3,141596
f = frequência (hertz)
L =
Indutância (henry)
3.10.7.1 A reatância
indutiva resulta da força
eletromotriz gerada através de uma bobina pela corrente alternada. O
valor instantâneo dessa tensão induzida aumenta e diminui conforme a
taxa de variação da corrente alternada aplicada aumenta e diminui,
conforme mostrado na Figura 3. A tensão está em seu valor máximo quando
a taxa de variação da corrente está em seu máximo; isso ocorre quando o
valor da corrente está em zero. Por outro lado, a tensão é zero quando
a taxa de variação da corrente é zero; isso ocorre quando a corrente
está em seu valor máximo. Considerando 360 graus como um ciclo
completo, a tensão induzida está adiantada em relação à corrente (por
exemplo, está fora de fase com a corrente) em 90 graus, conforme
ilustrado na Figura 3. A tensão induzida está em oposição à força
eletromotriz aplicada à bobina, reduzindo a amplitude da corrente
resultante.
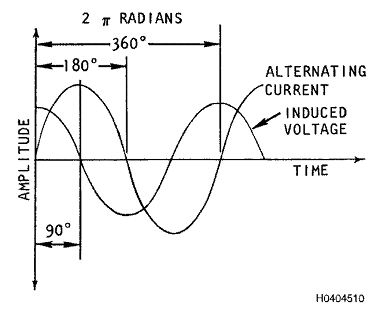
Figura 3.3. Variação Senoidal da Corrente Alternada e da
Tensão Induzida em uma Bobina
3.10.8 Combinando Grandezas
Fora de Fase.
Uma bobina real possui um componente resistivo da impedância, além da
reatância indutiva. Elas podem ser combinadas para descrever a
impedância líquida. Uma bobina pode ser considerada um resistor em
série com um indutor. A aplicação de uma corrente alternada a esse
circuito em série resultará em duas tensões, uma no resistor e outra no
indutor. A tensão líquida na combinação do resistor e do indutor (por
exemplo, em uma bobina real) será a combinação das duas tensões. A
tensão no resistor estará em fase com a corrente, enquanto a tensão no
indutor estará adiantada em relação à tensão no resistor em 90 graus. A
combinação das duas tensões, conforme ilustrado na Figura 4, resulta em
uma tensão que estará fora de fase com a corrente, mas não em 90 graus
completos.
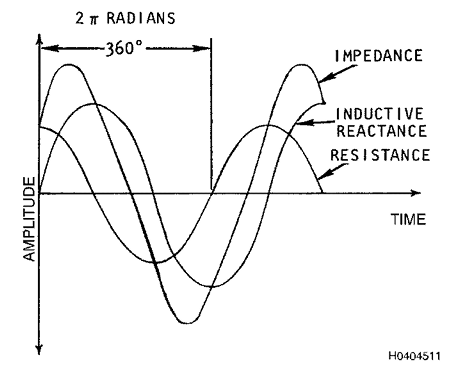
Figura 3.4. Combinação de Tensões Fora de Fase
3.10.8.1 Representação do
Gráfico XY (Diagrama Fasorial ou Plano de
Impedâncias).
Outra maneira de ilustrar a combinação de grandezas fora de fase em uma
bobina é ilustrada na Figura 5. Aqui, as duas quedas de tensão; uma
através do resistor (VR) e a outra através do indutor (VL) são plotadas
em ângulos retos entre si. Isso representa as duas grandezas estando 90
graus fora de fase. A combinação das duas grandezas é representada pela
linha diagonal OA que está no ângulo em relação à queda de tensão
através do resistor.
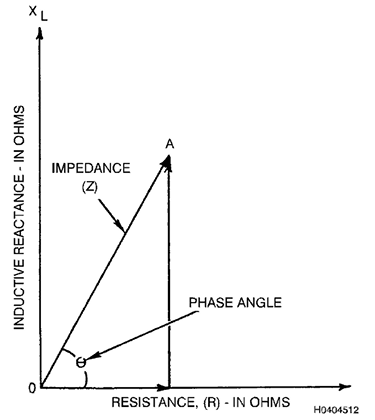
Figura 3.5. Diagrama Vetorial Mostrando a Relação
entre Resistência, Reatância e Impedância
3.10.8.2 Representação do
Plano de Impedância.
Assim como as duas tensões podem ser combinadas para produzir a tensão
líquida através de uma bobina (Figura 6); os componentes de impedância
resistiva e indutiva podem ser combinados para produzir a impedância
líquida de uma bobina. Na Figura 5, a reatância indutiva (XL)
é plotada
no eixo y e a resistência (R) é plotada ao longo do eixo x. Esses dois
valores definem a impedância representada pelo vetor OA.O valor do
ângulo é o mesmo que o ângulo da impedância líquida ilustrado na Figura
6 para a tensão líquida. Isso é importante porque mostra que a
impedância de uma bobina pode ser representada como a combinação de
duas quedas de tensão fora de fase. A amplitude da impedância pode ser
determinada a partir dos valores conhecidos de resistência e reatância
indutiva, de acordo com a seguinte fórmula:
Z = (XL2 + R2)1/2
Onde:
Z = Intensidade da Impedância (ohms)
XL = Reatância Indutiva (ohms)
R = Resistência (ohms)
XC = 0 (Reatância Capacidiva é desprezível)
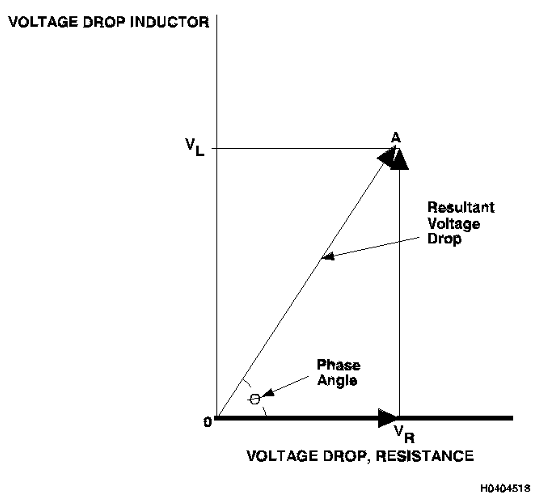
Figura 3.6. Diagrama mostrando a
relação das quedas de tensão na resistência da bobina e na reatância da
bobina
3.10.8.3 O ângulo de fase (
) da impedância pode ser calculado a partir
dos valores de resistência e reatância indutiva da seguinte forma:
Tan θ = XL / R
Onde:
θ = Ângulo de Fase (graus)
XL = Reatância Indutiva (ohms)
R = Resistência (ohms)
3.11 Diagramas de Impedância.
3.11.1 Objetivo.
O diagrama de impedância mostra como as mudanças nas variáveis de
ensaio de correntes parasitas mudam a impedância aparente de uma
bobina.
As variáveis típicas exibidas são condutividade elétrica,
permeabilidade magnética relativa, fator enchimento ou lift-off,
espessura da peça e frequência de ensaio. Os diagramas de impedância
são
muito úteis para determinar parâmetros de inspeção ideais e entender os
resultados de correntes parasitas quando mais de uma variável está
mudando. A representação vetorial da reatância indutiva no eixo y e da
resistência no eixo x da Figura 7 é a base do diagrama de impedância.
Deixe o ponto A representar a impedância de uma bobina de ensaio
enquanto estiver em uma peça. Se a sonda for movida para um local na
peça com uma descontinuidade, a impedância mudará. Essa nova impedância
pode ser
representada pelo ponto B, como mostrado na Figura 7. Cada mudança na
impedância criará um novo ponto no diagrama.
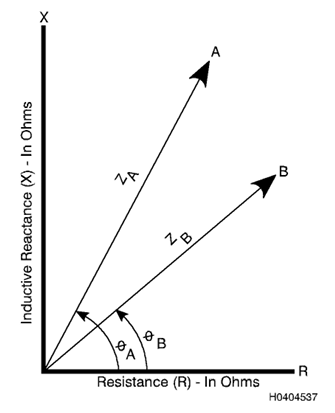
Figura 3.7. Representação
Vetorial da Impedância
3.11.2 Desenvolvimento de
um Diagrama de Impedância.
Para tornar o diagrama de impedância uma ferramenta útil para a
compreensão dos ensaios por correntes parasitas, é necessário alterar
sistematicamente um único parâmetro de ensaio, como a condutividade, e
observar as alterações na impedância (NT: Trabalhando com tela do tipo
plano de impedâncias [par cartesiano - duas dimensões], não é possivel
analisar mais de um parâmetro de ensaio por vez). Utilizando um
instrumento de
correntes parasitas com um visor gráfico bidimensional, uma sonda de
superfície, um pedaço de ferrite (uma cerâmica ferromagnética não
condutiva) e várias amostras de metal não magnético representando uma
faixa de condutividade de baixa (titânio, Inconel) a alta (cobre,
prata), diagramas de impedância aproximados podem ser desenvolvidos e
demonstrados. As amostras devem ter superfícies limpas, planas e nuas.
Quando a sonda de correntes parasitas é mantida afastada da peça (no
ar) e o instrumento é anulado, uma indicação (ponto) aparecerá no
visor. O ponto nulo pode ser reposicionado próximo ao canto superior
esquerdo da tela, conforme indicado pelo ponto A na Figura 8 e na
Figura
9. O ponto nulo no ar será usado como ponto de referência para o
restante dos diagramas (NT: Ponto de balanço ou Ponto de Trabalho). Em
seguida, a amostra de ferrite é usada para
estabelecer a direção da mudança indutiva. Coloque a sonda na ferrite e
ajuste o controle de fase de modo que a mudança do ar para a ferrite
seja vertical (paralela ao eixo y). Quando a sonda é colocada na
amostra de cobre, o ponto se moverá para um novo local na tela,
representado pelo ponto I na Figura 9. Conforme a sonda é levantada da
amostra, o ponto se moverá de volta para o ponto nulo no ar (A),
conforme mostrado na Figura 8 e na Figura 9. O caminho que a indicação
segue conforme a sonda é movida para contactar e para se afastar da
amostra é
chamado de traço/linha de elevação (NT: Também conhecido com Curva ou,
do Latim, "locus").
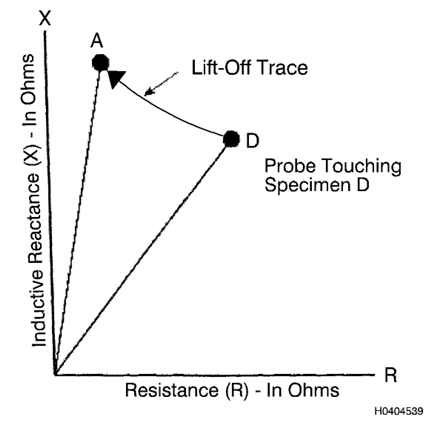
Figura 3.8. Representação vetorial de
uma mudança de impedância devido à decolagem
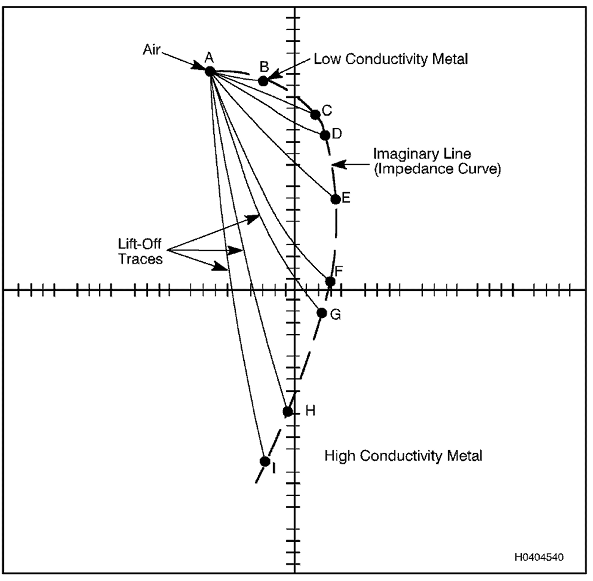
Figura 3.9. Diagrama de
impedância ilustrando os efeitos da condutividade variável
3.11.3 Usos típicos de um
diagrama de impedância.
O diagrama de impedância (mostrado na Figura 9) ilustra que a curva de
condutividade pode ser usada para medir a condutividade relativa de um
material desconhecido, comparando a posição de sua indicação na curva
de condutividade com as posições das indicações de materiais
conhecidos. Observe também que as curvas de lift-off estão em uma
direção diferente da curva de condutividade. Diz-se que mudanças na
condutividade e no lift-off têm ângulos de fase diferentes. Essa
diferença de ângulo de fase é ilustrada com mais detalhes na Figura 10.
A curva de lift-off também pode ser usada para medir a espessura de
revestimentos não condutores em uma superfície condutora. Isso é feito
comparando a distância na curva de lift-off para uma espessura de
revestimento desconhecida com distâncias na curva de lift-off
para espessuras conhecidas.
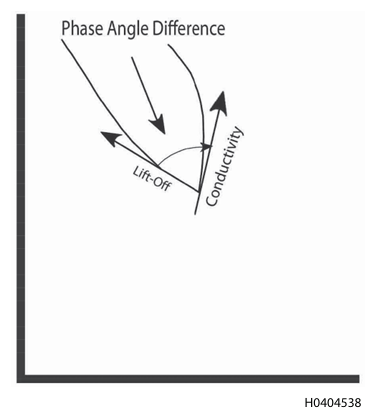
Figura 3.10. Diferença de Ângulo de Fase
3.11.4 Curva de
Condutividade.
Os controles de ganho e fase podem ser ajustados para colocar o ponto I
em qualquer lugar da tela. Como o cobre tem alta condutividade, será
conveniente ajustar o ganho para colocar o ponto I na parte inferior da
tela (Figura 9). Quando a sonda é colocada sobre as outras amostras de
metal, os respectivos pontos de impedância "B a H" (Figura 9) são
registrados. Observe que para cada um dos diferentes materiais, o ponto
estará localizado em um local diferente na tela (por exemplo, cada
amostra diferente tem uma impedância diferente). Cada linha do ponto
nulo A até o ponto de impedância para uma amostra específica representa
um traço de lift-off. Se uma curva suave for desenhada do ponto nulo A
através de cada um dos pontos de impedância B a I, uma curva de
condutividade será formada. O ponto na curva mais próximo do ponto nulo
do ar representa o material com a menor condutividade (por exemplo,
titânio). O ponto na curva mais distante do ponto nulo do ar representa
o material com a maior condutividade (cobre de alta pureza). Este
diagrama também mostra a condutividade relativa dos outras amostras.
3.11.5 Variações de
Espessura.
Quando a espessura da peça é menor que a profundidade efetiva de
penetração da bobina de ensaio na frequência de inspeção empregada, a
curva de impedância se afasta da curva de condutividade, conforme
mostrado na Figura 11. Tipicamente, há um aumento no componente
resistivo da impedância com peças mais finas, em comparação com peças
que têm espessura igual ou maior que a profundidade efetiva de
penetração. À medida que a espessura das peças aumenta e se aproxima
mais do limite efetivo de penetração, a curva tende a espiralar à
medida que se aproxima do ponto final (T = 1) na curva de
condutividade, onde T é igual à razão entre a espessura da amostra e a
profundidade efetiva de penetração naquela amostra.
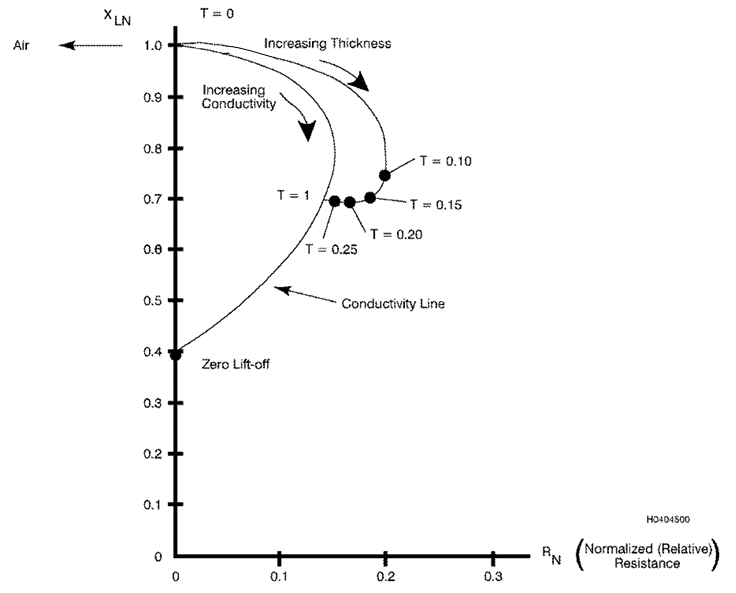
Figura 3.11. Diagrama
de Impedância Mostrando o Efeito da Espessura da Amostra
3.11.6 Camadas Condutoras.
A curva de impedância para camadas condutoras finas em um substrato de
condutividade diferente também é representada como uma mudança na curva
de impedância para condutividade.A impedância para o material em
camada parte da curva de condutividade no valor correspondente à
condutividade do substrato e forma uma nova curva que se junta à curva
de
condutividade no valor da condutividade do metal da camada externa. O
aumento da
espessura da camada externa corresponde a uma direção horária ao longo
dessa curva. O ponto em que a curva correspondente a camada externa se
junta à curva da camada interna representa a
profundidade efetiva de penetração na camada externa.
3.11.7 Normalização da Impedância.
Para ilustrar os princípios
gerais da inspeção por correntes parasitas
ou para apresentar dados de forma universal, independente de valores
específicos de impedância da bobina, os diagramas de impedância são
geralmente normalizados. Na normalização, a reatância indutiva (eixo
vertical, Y) e a
resistência (eixo horizontal, X) da bobina na peça são divididas pelo
valor da reatância
indutiva da bobina no ar. Portanto, o eixo vertical do diagrama de
impedância é igual à reatância indutiva relativa (XLN) da
bobina de
ensaio; e o eixo horizontal do diagrama de impedância é igual à
resistência relativa (RN) da bobina de ensaio. A
normalização é um
método conveniente para permitir comparações de dados de correntes
parasitas de um grande número de ensaios usando diferentes sondas e
materiais. As formas dos diagramas de impedância permanecem as mesmas.
No entanto, o ponto nulo do ar A na Figura 12 torna-se 1 no eixo Y do
diagrama de impedância após a normalização. Os diagramas de impedância
neste manual serão todos representados pela reatância normalizada
(XLN), no eixo Y e pela resistência normalizada (RN)
no eixo X.
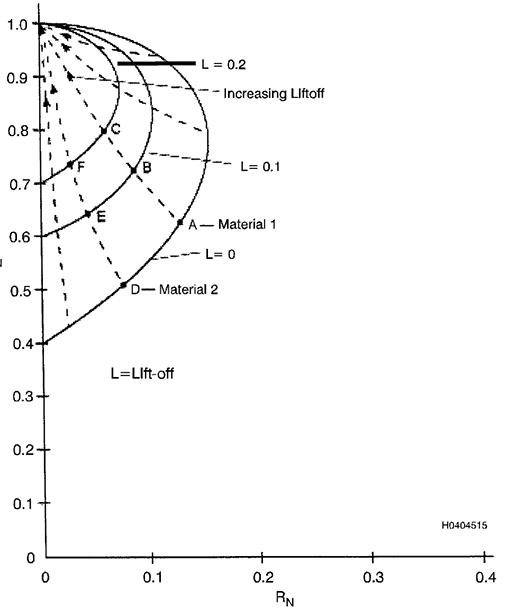
Figura
3.12. Diagrama de Impedância Mostrando o Efeito do Lift-Off
3.12 Análise do Plano de
Impedância.
A maioria das aplicações de correntes parasitas tem dois grandes
problemas a superar. O primeiro é ignorar mudanças em parâmetros não
interessantes (considerados ruído) durante o ensaio; um exemplo é a
variação do lift-off
durante a inspeção de trincas. O segundo é reconhecer indicações
válidas enquanto outras mudanças estão ocorrendo. Outra maneira de
afirmar isso é que variações insignificantes, como aquelas associadas
ao lift-off, não devem ser confundidas com indicações válidas de
defeitos, e indicações válidas de defeitos não devem ser ocultadas por
alterações irrelevantes, como o lift-off. A análise do plano de
impedância, também chamada de análise de fase (NT: porque as fases das
indicações são diferentes), é uma ferramenta eficaz
na solução desses problemas.
3.12.1 Detecção de Fase.
Medições do ângulo de fase são uma boa maneira de detectar uma
variedade de condições de falhas. As informações no diagrama vetorial
(Figura 5) ilustram isso. Reduções de condutividade (por exemplo,
trincas) e permeabilidade podem produzir a mesma amplitude de sinal, e
seria difícil diferenciar entre trincas e mudanças normais de
permeabilidade em uma peça. No entanto, o ângulo de fase de uma mudança
de condutividade é muito diferente de uma mudança de permeabilidade se
a frequência de ensaio correta for escolhida. Usando técnicas de
detecção de fase, torna-se simples detectar a diferença entre variações
de permeabilidade e trincas. Isso também se aplica à determinação da
profundidade de uma falha, que é sensível à fase.ou separar os efeitos
de lift-off das condições de falha. Os detectores sensíveis à fase usam
uma variedade de técnicas, como divisores de fase, deslocadores de
fase, média, detecção de meia onda e onda completa, amostragem e
técnicas subtrativas e aditivas. A apresentação da impedância
nos instrumentos de corrente parasita com tela de forma de onda; usa
detectores sensíveis a duas fases para fornecer detecção de fase
horizontal e vertical (NT: Os aparelhos que apresentam sinais senoidais
atualmente praticamente não são mais utilizados). Essas informações são
combinadas para produzir
um ponto na tela (NT: O autor voltou aqui a falar em aparelhos com tela
apresentando um ponto representativo da impedância) que representa a
fase e a amplitude relativas de um
sinal de corrente parasita. Alguns tipos de instrumentos de medição
utilizam um controle de fase ajustável ou área selecionável ("gate") de
fase na tela para permitir
apenas a detecção do sinal em um ângulo de fase específico de
interesse.
3.12.2 Trincas, Lift-Off e
Condutividade.
A impedância muda devido a trincas superficiais de diferentes
profundidades. A mudança para trincas estará entre mudanças do lift-off
e da
condutividade. À medida que a profundidade da trinca aumenta, a
resposta se afasta do lift-off e se aproxima da condutividade
decrescente.
3.12.3 Detecção de Trincas
em Materiais Não Ferromagnéticos.
A amplitude da resposta de uma trinca superficial aumenta à medida que
a trinca se aprofunda. Quando a trinca atinge três profundidades padrão
(Parágrafo 3.4.1), ela interrompe essencialmente todo o fluxo de
correntes parasitas e nenhum aumento na amplitude é observado à medida
que se aprofunda ainda mais. Além de um aumento de amplitude para
trincas mais profundas, o ângulo de fase da indicação da trinca muda.
Uma trinca rasa interrompe pouco do fluxo de correntes parasitas, então
a amplitude do seu sinal é pequena. Além disso, é essencialmente uma
condição de superfície, então a direção (fase) da resposta do sinal é
muito próxima daquela do lift-off (Figura 13). Uma trinca mais profunda
interrompe mais do fluxo de correntes parasitas, então seu sinal tem
maior amplitude. Ela se estende bem abaixo da superfície, a direção
(fase) do seu sinal é mais distante do lift-off (Figura 14). A trinca
de três profundidades padrão tem a maior resposta de amplitude. Ele
interrompe as correntes parasitas tão profundamente no metal quanto o
ensaio pode detectar, parece uma mudança na propriedade de volume de
menor condutividade, e a direção do sinal da trinca (fase) é ao longo
da curva de condutividade (Figura 15).
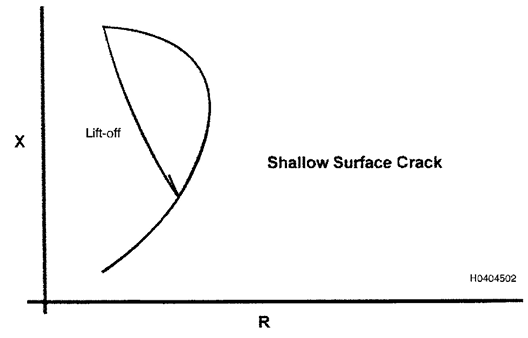
Figura 3.13. Trinca de superfície
rasa
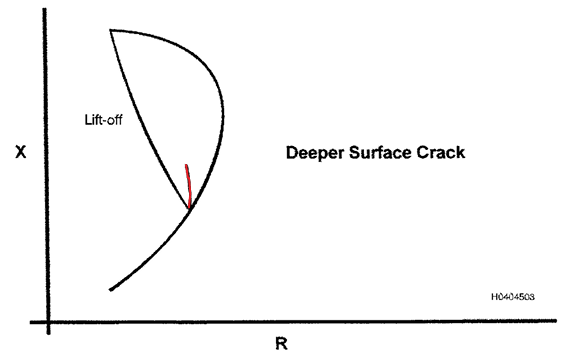
Figura 3.14. Trinca de superfície mais profunda
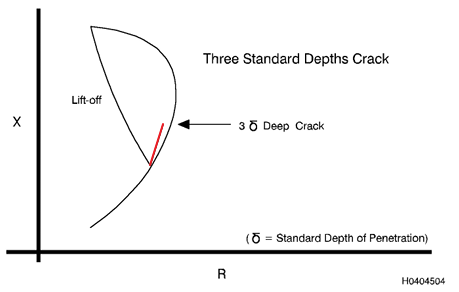
Figura 3.15. Três
profundidades padrão de penetração
3.12.3.1 Para trincas com
profundidade maior que três profundidades padrão não alterará a
resposta do sinal porque não haverá fluxo de corrente
parasita para interromper. No entanto, haverá uma mudança na resposta
do sinal para uma trinca interna (subsuperficial). Primeiro, as
correntes parasitas
fluirão sobre o topo da trinca (na superfície), a trinca interna
não bloqueará tanto o fluxo de correntes parasitas e a amplitude do
sinal deve diminuir. Segundo, a trinca agora está mais distante da
superfície, então seu ângulo de fase ainda deve estar mais distante do
lift-off (Figura 16).
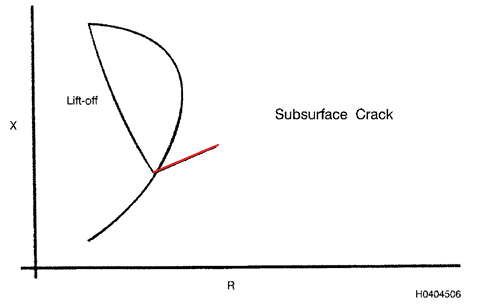
Figura 3.16. Trinca Subsuperficial
3.12.3.2 A resposta do
sinal diminui à medida que a profundidade da
trinca abaixo da superfície aumenta.À medida que o defeito
subsuperficial se afasta da superfície, a amplitude do sinal diminui e
o ângulo de fase gira no sentido horário, afastando-se do sinal de
lift-off (Figura 17).
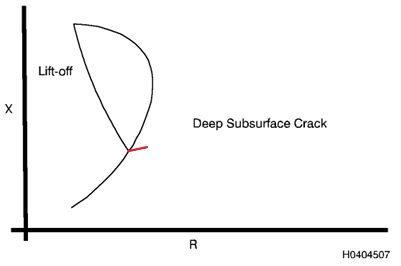
Figura 3.17. Trinca Subsuperficial Profunda
3.13 Atraso de Fase (Defasagem) em Profundidade.
Uma mudança no ângulo de fase ocorre devido a alteraração do tempo no
campo
de correntes parasitas pela maior distância percorrida. Alterações na
superfície da peça são vistas imediatamente pela bobina, enquanto
perturbações no campo em alguma profundidade na peça requerem algum
tempo de viagem para retornar à superfície, onde são vistas pela
bobina. Eletricamente, isso é descrito como atraso de fase em
profundidade, e a quantidade de atraso de fase é de 1 radiano (57°) por
cada profundidade padrão de penetração (Figura 18). Esse atraso de fase
do
sinal com relação ao sinal de lift-off (superfície) pode ser usado para
medir a
profundidade dos defeitos. O ângulo de fase de um sinal de defeito se
correlaciona com a profundidade do defeito.
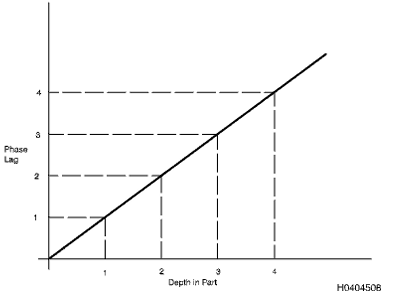
Figura 3.18. Atraso de Fase e
Profundidade na Parte
3.14 Efeitos das Condições de Inspeção na Inspeção por Correntes
parasitas.
3.14.1 Frequência.
A intensidude das correntes parasitas induzidas na peça aumenta (mais
fortemente na superfície) à medida
que a frequência da corrente indutora aumenta. Por sua vez, as
correntes parasitas de maior intensidade geram um campo magnético
oposto mais forte, reduzindo a penetração do campo primário. Portanto,
mantendo-se todos os outros fatores constantes, frequências mais altas
resultam em profundidades de penetração menores, como mostrado na
Figura 19.
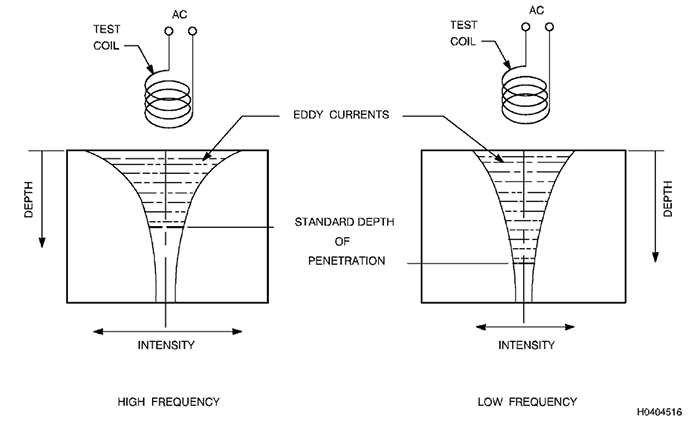
Figura 3.19. Efeito Relativo da Frequência na Profundidade de
Penetração.
3.14.2 Condutividade e
Frequência.
Existe uma relação entre condutividade e frequência de inspeção ideal.
Como exemplo, uma inspeção por correntes parasitas para trincas na liga
de alumínio 7075-T6, com uma condutividade de cerca de 30% IACS,
utiliza uma frequência de 200 kHz. Para realizar uma inspeção com
profundidade de penetração comparável em uma liga de titânio, TI
6Al-4V, com uma condutividade de cerca de 1% IACS, seria necessária uma
frequência de cerca de 6 MHz.
3.14.3 Acoplamento
Eletromagnético (Efeito Lift-off).
A interação entre o campo eletromagnético primário gerado pela bobina e
o artigo inspecionado é chamada de acoplamento eletromagnético. Como a
intensidade do campo diminui com o aumento da distância da bobina a
peça, as
correntes parasitas resultantes na superfície da peça também diminuem
de intensidade. Um termo de engenharia elétrica que também pode ser
usado é acoplamento indutivo (NT: O efeito manifestado na tela do
aparelho por esse fenômeno é o sinal de lift-off).
3.14.4 Fator de Enchimento.
Quando uma bobina envolvente é usada para inspecionar uma peça de
formato cilíndrico, o grau de acoplamento magnético depende da
diferença entre o diâmetro interno da bobina e o diâmetro externo da
peça. Esse efeito é denominado fator de enchimento. Para bobinas
internas, o acoplamento eletromagnético (indutivo) é determinado pela
folga de ar entre o diâmetro externo da bobina e o diâmetro interno que
está sendo inspecionado. O fator de enchimento é calculado usando a
fórmula básica, mas neste caso di é o diâmetro interno da peça e Do é
o diâmetro externo da bobina colocada no orifício da peça (Parágrafo
8.3).
3.14.5 Corrente da Bobina.
Com todos os outros fatores constantes, um aumento na corrente que flui
através da bobina resulta em uma maior intensidade do campo magnético e consequentemente na corrente parasita gerada.
3.14.6 Temperatura.
A temperatura na qual uma inspeção é realizada afeta tanto a
condutividade elétrica quanto as propriedades ferromagnéticas do artigo
sob inspeção. A condutividade elétrica geralmente diminui com o aumento
da temperatura e, inversamente, aumenta com a diminuição da
temperatura. A redução em temperaturas mais altas ocorre devido ao
espalhamento de elétrons de condução por átomos que se movem com
oscilações térmicas aumentadas. Os efeitos da temperatura nas
propriedades ferromagnéticas de um material são geralmente
insignificantes, com uma exceção. Acima de uma temperatura específica
chamada temperatura de Curie (cerca de 1400 °F ou 760 °C), as
propriedades ferromagnéticas desaparecem. Devido aos efeitos térmicos
na condutividade, o aumento da temperatura do artigo sob inspeção
diminui ligeiramente a intensidade das correntes parasitas na
superfície de uma peça e aumenta ligeiramente a profundidade de
penetração. Variações de temperatura também afetam a indutância da
bobina. Lembre-se de que mudanças na temperatura afetam os resultados
do ensaio de CP. Portanto, durante as inspeções, DEVE-SE permitir um
tempo para
que o sistema de ensaio e a peça de ensaio se estabilizem à temperatura
ambiente. Um exemplo de ensaio seria verificar se a peça e os padrões
têm a mesma sensação ao toque.
3.14.7 Geometria.
Características geométricas como bordas, superfícies curvas, alterações
na espessura e revestimentos não condutores (como tinta) em superfícies
afetam a distribuição e a intensidade das correntes parasitas. À medida
que uma sonda se aproxima de uma borda, a resposta da corrente parasita
é conhecida como efeito de borda e parece semelhante à resposta de uma
trinca. Da mesma forma, superfícies irregulares e revestimentos não
condutores podem variar a distância entre a bobina da sonda e a peça.
Essas alterações são conhecidas como lift-off, e os efeitos
consequentes no sinal da corrente parasita são chamados de efeitos
lift-off. O lift-off geralmente não pode ser completamente evitado;
portanto, compensar algum lift-off faz parte do procedimento de
calibração. Variações na espessura da peça também podem produzir uma
resposta interferente em algumas unidades de corrente parasita quando a
espessura está na faixa da profundidade de penetração do campo da
corrente parasita.
3.14.8 Lift-Off.
Os efeitos do lift-off podem ser usados para medir a espessura do
revestimento. Alterações no lift-off podem ser calibradas para permitir
medições da espessura de revestimentos não condutores. O fator de
enchimento se aplica a peças que passam por uma bobina envolvente e,
de maneira semelhante ao lift-off, pode ser usado para medir algumas
dimensões. À medida que uma bobina de ensaio se afasta de uma peça
(aumentando o lift-off), o acoplamento entre a bobina de ensaio e a
peça
de inspeção diminui. A magnitude da alteração da impedância para uma
alteração específica em uma variável de inspeção também diminui. Para
sondas superficiais, as linhas pontilhadas que conectam pontos que
representam as mesmas propriedades do material, mas com diferentes
quantidades de lift-off, apresentam alguma curvatura, como mostrado na
Figura 12. A linha ABC representa o aumento do lift-off para o material
um.A linha DEF representa o aumento dao lift-off do material dois. A
linha do ponto A ao ponto D representa o aumento da condutividade do
material dois em comparação com o material para o mesmo valor de
lift-off.
As linhas de decolagem BE e CF são cada vez mais curtas, indicando uma
menor variação na condutividade (NT: Quanto maio o lift-off menor é a
sensibilidade do ensaio de correntes parasitas).

|

|
|