IAEA-Cp2-PrincipiosFisicos

IAEA Insternational Atomic Energy Agency

IAEA - Correntes Parasitas - Capítulo 2 - PRINCÍPIOS FÍSICOS DO ENSAIO

traduzido do livro: https://www.iaea.org/publications/8414/eddy-current-testing-at-level-2-manual-for-the-syllabi-contained-in-iaea-tecdoc-628rev-2-training-guidelines-for-non-destructive-testing-techniques

Capítulo 2 - PRINCÍPIOS FÍSICOS

2. PRINCÍPIOS FÍSICOS DO ENSAIO

2.1. Eletricidade

O estudo das cargas em movimento é chamado de eletricidade e a taxa de fluxo de carga é chamada de corrente elétrica. Quando a diferença de potencial elétrico entre duas cargas força uma terceira carga a se mover, a carga em movimento é uma corrente elétrica. Portanto, para produzir corrente, a carga deve ser movida por uma diferença de potencial. No caso de um condutor, a corrente é definida como o fluxo de elétrons através do condutor. Os elétrons são partículas carregadas negativamente que fazem parte do átomo, que é o elemento de construção básico de qualquer material. Alguns materiais são condutores, enquanto outros não. Um material é chamado de condutor se for capaz de conduzir a corrente elétrica. Um material condutor possui cargas livres, que se movem sob a influência de um campo externo. As cargas livres em um condutor metálico são elétrons negativos. As cargas livres em um eletrólito são íons, tanto positivos quanto negativos. Um gás em condições adequadas, como em um letreiro de néon ou lâmpada fluorescente também é um condutor e suas cargas livres são íons positivos e negativos e elétrons negativos.

2.1.1 Corrente contínua (CC)

Uma corrente elétrica que flui continuamente em um sentido através de um condutor é chamada de corrente contínua (CC). A pilha elétrica (bateria) é uma fonte de tensão CC porque possui apenas uma polaridade da tensão de saída que produz corrente contínua no circuito externo.

Amperagem e voltagem

Quando há um campo elétrico em um condutor, as cargas livres dentro dele são colocadas em movimento. Cargas positivas se movem na mesma direção do campo e cargas negativas se movem na direção oposta. FIG. 2.1 mostra uma porção de um condutor dentro da qual existe um campo elétrico de intensidade E. Em um condutor metálico, cargas negativas cruzando uma seção da direita para a esquerda são equivalentes a cargas positivas cruzando da esquerda para a direita. Toda a corrente é devida ao movimento das cargas livres. Os elétrons se movem na direção oposta à corrente convencional em um condutor metálico. O valor da corrente, I, é dado pela relação

I = Q / t (2.1)

onde:
I = corrente elétrica
Q = carga
t = tempo

Movimento dos elétrons num condutor

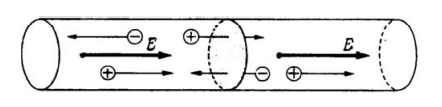
FIG. 2.1. Cargas positivas se movem na direção do campo em um condutor

A unidade de corrente no sistema de unidades MKS é um Ampere, que representa a quantidade de um Coulomb de carga fluindo por segundo. Quantitativamente é igual ao fluxo de 6,25 × 10¹⁸ elétrons por segundo através de um determinado ponto em um circuito. A unidade básica de potencial em um campo eletrostático é um Volt que é igual à diferença de potencial entre dois pontos para os quais um Coulomb de carga fará um Joule de trabalho indo de um ponto a outro, ou seja,

1 Volt = 1 Joule / Coulomb (2.2)

A relação acima nos ajuda a definir a diferença de potencial. Diz-se que a diferença de potencial (também chamada de tensão elétrica, ou popularmente voltagem) entre dois pontos (arbitrários) é de um Volt se o trabalho realizado para levar uma unidade de carga de um ponto a outro for um joule. Se os pontos estiverem com as letras A e B, a diferença de potencial entre eles é simplesmente V_A - V_B ou V_B - V_A. A diferença de potencial entre os terminais de uma bateria automotiva de chumbo é de cerca de 12 volts com o terminal marcado + em potencial mais alto. Se chamarmos este terminal de A e outro terminal (negativo) de B, então V_AB = 12 Volts e V_BA = - 12 Volts.

Existe um campo elétrico no espaço entre os terminais da bateria. Se a carga positiva se move do terminal A (+) para o terminal B (-), sua energia potencial diminui em 12 Joules/Coulomb. Essa energia aparece em alguma outra forma, como calor no filamento de uma luz incandescente ou como trabalho na partida do motor. A energia elétrica, derivada de energia mecânica, química ou outra forma de energia que deve ser aplicada através do material para forçar os elétrons a se moverem, é chamada de Força Eletromotriz (FEM). A diferença de potencial entre os terminais da bateria quando ela não está fornecendo corrente para um circuito externo é chamada de FEM. Quando um FEM é aplicado através de um material condutor, resulta em fluxo de corrente elétrica. A unidade de FEM também é um Volt.

Lei de Ohm e resistência

Se uma tensão V é aplicada em um condutor, uma corrente I flui através dele. George Ohm descobriu que a magnitude da corrente nos metais é proporcional à tensão aplicada, desde que não haja mudança no estado físico do condutor. Isso é conhecido como a lei de Ohm. A relação é exata dentro da precisão das medidas. Matematicamente, pode ser escrito como

I = V / R (2.3)

A resistência em qualquer material condutor é a medida da oposição ao movimento dos elétrons livres devido às suas colisões contínuas contra os átomos da rede. A resistência depende da natureza, dimensão e estado físico do condutor. A unidade de resistência elétrica é Ohm (Ω). O Ohm é definido como a resistência de um condutor através do qual uma corrente de um Ampere está fluindo quando a diferença de potencial através dele é de um Volt, ou seja

1 Ohm = 1 Volt / 1 Ampere

A quantidade de resistência em um material é um fator que limita a quantidade de corrente que flui através do material para uma determinada força eletromotriz (FEM) aplicada. Como a resistência em um circuito resulta no gasto de energia, o resultado é a dissipação dessa energia na forma de calor. Para um condutor puro, a resistência é diretamente proporcional ao seu comprimento L e inversamente proporcional à sua área de seção transversal A, ou seja

R α L / A
ou
R = ρ L / A (2.4)

onde:
R = resistência elétrica
ρ = resistividade elétrica do material
L = comprimento do condutor
A = seção reta do condutor

Condutividade e resistividade.

A condutividade é definida como a capacidade de um material conduzir corrente elétrica. É denotado por σ. A unidade de condutividade é Siemens por metro ou mho por metro. A condutividade de um condutor diminui com o aumento da temperatura. Cada elemento tem um valor único de condutividade. Cobre, prata e ouro têm alta condutividade, enquanto o carbono tem uma condutividade muito baixa.

Uma corrente parasita é um fluxo de elétrons. A quantidade de fluxo de elétrons através de um material eletricamente condutor está diretamente relacionada à condutividade do material. Se a condutividade aumenta, o fluxo de correntes parasitas aumenta.

A resistividade é recíproca (inverso) da condutividade. Portanto, os materiais que possuem alta resistividade possuem baixa condutividade e vice-versa. A resistividade é denotada por ρ e é definida como a relação da intensidade elétrica (FEM) para a corrente por unidade de área de seção transversal.

Matematicamente pode ser escrito como
Mathematically it can be written as

ρ = E / I / A

ou

ρ= E A / I (2.5)

onde
ρ = resistividade elétrica do material
E = força eletromotriz (FEM)
L = comprimento do condutor
A = seção reta do condutor

O valor da resistividade também pode ser derivado da relação (2.4), ou seja,

ρ = R A / L

A unidade de resistividade é Ohm-metro (Ω-m).

O Ohm-metro é uma unidade maior, a unidade menor é o micro Ohm-centímetro (µΩ-cm).

A resistividade de um material muda com a mudança de temperatura. À medida que a temperatura do condutor aumenta, a amplitude da vibração dos átomos na rede aumenta e, portanto, a probabilidade de sua colisão com os elétrons livres também aumenta. Pode-se dizer também, que em altas temperaturas, os átomos oferecem maior área alvo, ou seja, a seção transversal de colisão dos átomos aumenta. Isso faz com que a colisão entre os elétrons livres e os átomos na rede seja mais frequente e, portanto, a resistência do condutor aumenta.

Experimentalmente, a mudança na resistividade de um condutor metálico com a temperatura é quase linear em uma ampla faixa de temperaturas abaixo e acima de 0°C. Nessa faixa, a mudança fracionária na resistividade por Kelvin é conhecida como o coeficiente de resistividade da temperatura.

Em ensaios de correntes parasitas, a condutividade é frequentemente dada como uma porcentagem do padrão internacional de cobre recozido puro (%IACS = International Annealed Cooper Standard). Neste sistema, a condutividade do cobre puro recozido a 20°C é considerada 100% e a condutividade de outros materiais é dada como uma porcentagem da condutividade do cobre. A condutividade de um material pode ser calculada a partir de sua resistividade.

%IACS = 172.41 / ρ (2.6)

onde
IACS = International Annealed Copper Standard (Padrão de ferro recozido puro)
ρ = resistividade elétrica do material (µΩ-cm)

A condutividade é uma das principais variáveis na inspeção de correntes parasitas. Possibilita a triagem de certos materiais com base em sua condutividade, a detecção de mudanças na química, distorção da rede, tratamento térmico, dureza, descontinuidades, etc. A resistividade e a condutividade de vários materiais são dadas na Tabela 2.1.
Conductivity is a one of main variables in eddy current inspection. It makes possible the screening of certain materials based upon their conductivity, the detection of changes in chemistry, lattice distortion, heat treat, hardness, discontinuities, etc. The resistivity and conductivity of various materials are given in Table 2.1.

TABLE 2.1. VALORES DE RESISTIVIDADE E DE CONDUTIVIDADE DE VÁRIOS MATERIAIS

Material	Resistividade (μΩ-cm), x 10^-7	Condutidade (mho/m), x 10⁷	Condutividade (%IACS)
Prata	1,6	6.14	105
Cobre	1,7	5,81	100
Ouro	2,4	4,10	70
Alumínio	2,8	3,55	61
7075-T6 (liga Al)	5,3	1,89	32
Zincco	5,9	1,70	29
Magnésio	4,6	2,17	37
Latão Almirantado	7,0	1,43	24
Ferro	9,7	1,03	18
Bronze Fosforoso	16	0,63	11
Chumbo	20,6	0,49	8,4
Cu-Ni 70-30	37,4	0,27	4,5
Monel	48,2	0,21	3,6
Zircônio	50	0,20	3,4
Titânio	54,8	0,18	3,1
Aço Inox 304	70	0,14	2,5
Sircalloy-2	72	0,14	2,5
Inconel 600	98	0,10	1,7
Hastelloy X	115	0,087	1,5
Waspalloy	123	0,081	1,4
Ti-6A I-4V	172	0,058	1,0

2.1.2 Corrente alternada (AC)

Uma corrente elétrica que inverte sua direção de fluxo em intervalos regulares é chamada de corrente alternada (CA). Os circuitos CA são de grande importância na eletricidade aplicada. A corrente alternada é tanto positiva quanto negativa. Uma onda senoidal típica mostrando a tensão CA é mostrada na FIG. 2.2 abaixo. A tensão alternada inverte periodicamente a polaridade, causando a corrente alternada que inverte periodicamente sua direção.

Onda senoidal representando CA

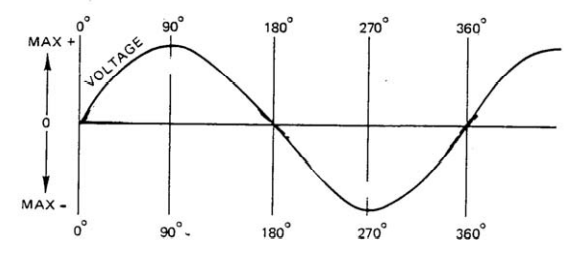
FIG. 2.2. Curva de onda senoidal mostrando a tensão CA.

Amplitude e Fase

Os sistemas que variam periodicamente uma determinada propriedade com o tempo são chamados de sistemas de variação de tempo sinusoidal. Os circuitos elétricos tendem a desenvolver correntes e tensões que variam senoidalmente, ou têm respostas particularmente simples a sinais senoidais. Para manter uma corrente contínua em um condutor, o campo elétrico deve ser mantido, ou seja, a diferença de potencial através do condutor deve ser mantida. Se o campo inverte sua direção periodicamente, o fluxo de carga se inverte e a corrente alterna entre os dois valores máximos positivos e negativos máximos constantes. Isso está ilustrado na figura. 2.3. A altura vertical máxima da onda é chamada de amplitude. A tensão muda sua amplitude a cada meio ciclo e um tempo igual para atingir o valor máximo de amplitude negativa.

O tempo necessário para completar um ciclo é denominado período e o número de ciclos por segundo é chamado de frequência. A unidade de frequência é Hertz (Hz), que é igual a 1 ciclo por segundo. Na curva de onda senoidal mostrada acima ao longo do eixo X, temos o ângulo de fase em radianos ou graus, enquanto o eixo Y representa a amplitude em um determinado momento. Em π/2 ou 90° temos a máxima amplitude positiva da forma de onda, enquanto em 3π/2 ou 270° temos a máxima amplitude negativa da forma de onda. O ângulo subtendido por qualquer ponto da curva até sua posição inicial é chamado de ângulo de fase. Em qualquer instante t, a tensão instantânea V(t) é dada por

V(t) = V_o sen(ωt) = V_o sen(2πft), (2.7)

Onde
V(t) = voltagem instantânea
V_o = voltagem inicial
ω = frequência angular
t = tempo
f = frequência

N.T.: Como, teoricamente, o ciclo se repete perenemente, muitas vezes é representado sob a forma de circulo, também conhecido como diagrama fasorial.

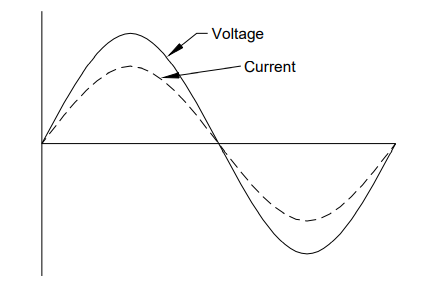
FIG. 2.3. Voltagem e corrente em fase.

Defasagens corrente-voltagem

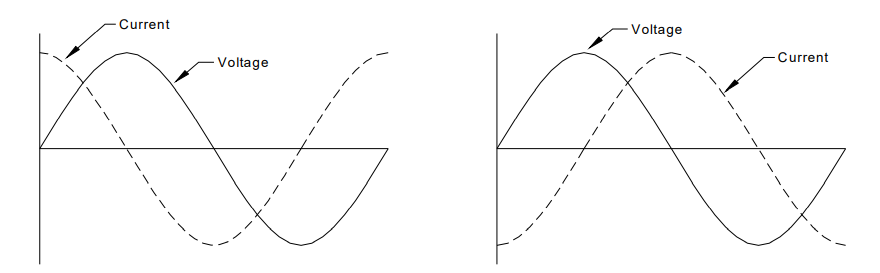
FIG. 2.4. Defasagem entre corrente e voltagem:
a. Corrente adiantada da voltagem em 90°;
b. Corrente atrasada da voltagem em 90°.

Ângulos de fase

Embora a onda senoidal mostrada na FIG. 2.2 pode ser usado para representar a corrente ou a tensão, se a corrente e a tensão devem ser mostradas, então são necessárias duas ondas senoidais. Quando as ondas senoidais da corrente e da tensão passam pelo zero na mesma direção e ao mesmo tempo, diz-se que a tensão e a corrente estão em fase uma com a outra, como mostrado na FIG. 2.3. No entanto, como será discutido posteriormente, a corrente e a tensão podem não estar em fase uma com a outra. A corrente pode estar adiantada ou atrasada em relação tensão. A quantidade de avanços ou de atrasos da corrente, com relação a tensão, podem ser expressos em graus ou tempo, conforme mostrado na FIG. 2.4.

Efeito da resistência pura

Quando uma corrente alternada é passada através de uma resistência isolada (chamada, pura), a corrente pode ser calculada dividindo a tensão pela resistência. Como a resistência é constante, a corrente terá um valor proporcional à tensão. Como a tensão (CA) está mudando continuamente, tanto em intensidade quanto em direção, a corrente mudará de maneira semelhante. Portanto, as curvas de tensão e corrente subirão e descerão juntas, conforme mostrado na FIG. 2.5 e são ditos 'em fase' na mesma frequência. No entanto, como o valor da resistência afeta o fluxo de corrente, as amplitudes da tensão e da corrente podem ser diferentes de acordo com a Lei de Ohms. O valor da resistência não é afetado por uma mudança na frequência.

Circuito resistivo puro

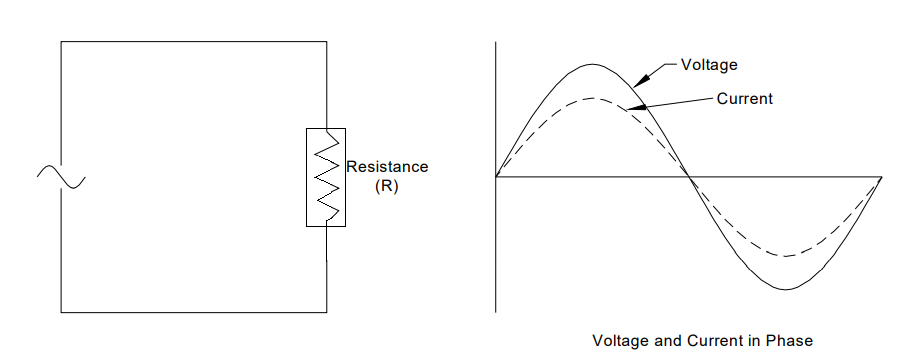
FIG. 2.5. Circuito apenas com resistência (resistência pura).

Efeito da indutância pura

A indutância, como a resistência, impõe um limite na corrente que uma dada tensão CA fará fluir em um circuito. A magnitude da oposição ao fluxo de corrente por uma indutância é chamada de reatância indutiva (X_L), que, ao contrário da resistência, varia com a frequência. Se a frequência for zero (CC), não há indutância e uma bobina atuará como um condutor comum, mas à medida que a frequência aumenta (CA), a taxa de variação do campo magnético da bobina aumenta e a bobina se tornará cada vez mais indutiva , aumentando assim a oposição ao fluxo de corrente. Portanto, quanto maior a frequência, maior a reatância indutiva. Como a indutância é uma propriedade magnética dependente da taxa de variação da corrente, em um circuito puramente indutivo (onde se assume que não há resistência), a corrente ficará atrasada em relação à tensão em 90°, conforme mostrado na FIG. 2.6. Isso é explicado ainda mais pela apreciação de que o campo magnético está mudando em cada ciclo em sua taxa máxima de mudança quando a tensão é zero. À medida que a tensão passa por zero em cada ciclo, a FEM induzida (oposta) é máxima. A reatância indutiva, como a resistência, é medida em Ohms.

X_L = 2πfL (2.8)

Onde
X_L = reatância indutiva
f = frequência
L = indutância

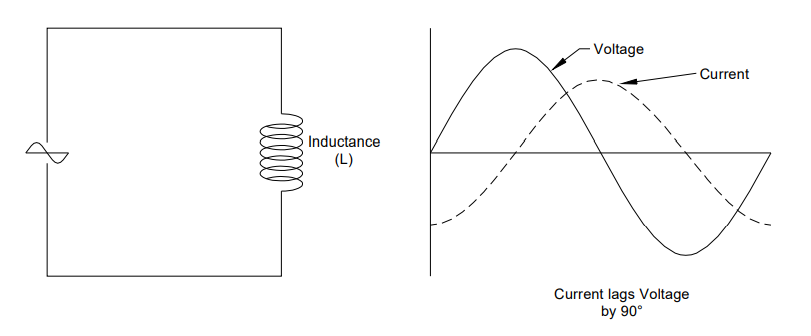
FIG 2.6. Circuito com indutância pura. Corrente atrasada em realação a Tensão.

Efeito da capacitância pura

Em um circuito CC, um capacitor totalmente carregado atua como uma interrupção completa e nenhuma corrente fluirá. No entanto, em um circuito CA, o capacitor está continuamente sendo carregado e descarregado à medida que a tensão se alterna. Como pode ser visto na FIG. 2.7, quando a tensão está em seu valor máximo, o capacitor está totalmente carregado e nenhuma corrente fluirá. Quando a tensão cai, o capacitor descarrega e a corrente estará em seu valor máximo quando a tensão for zero. À medida que a tensão aumenta novamente, a corrente diminui e assim por diante. Portanto, em um circuito puramente capacitivo (onde se supõe que não há resistência), a corrente está adiantada da tensão em 90°. Pode-se considerar a analogia de um acumulador hidráulico sendo carregado e descarregado. À medida que a bomba arranca e o acumulador está vazio, o fluxo é máximo com pressão mínima. Capacitância, como resistência e indutância, impõe um limite na corrente a uma dada tensão CA que faz a corrente fluir em um circuito. A magnitude da oposição ao fluxo de corrente por uma capacitância é chamada de reatância capacitiva (X_C) e é medida em Ohms. A reatância capacitiva também varia com a frequência, mas ao contrário da reatância indutiva, quanto maior a frequência, menor a reatância capacitiva.

X_C = 1 / (2πfC)

Onde
X_C = reatância capacitiva
f = frequência
C = capacitância

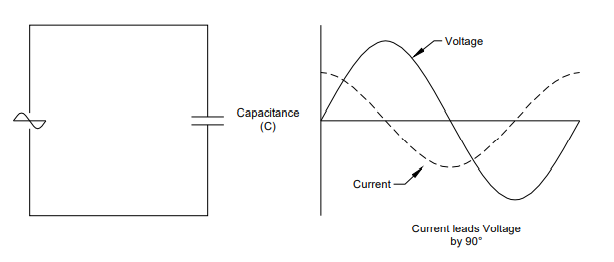
FIG. 2.7. Circuito com capacitância pura. Tensão atrasada em relação a corrente.

Frequência de ressonância

Se um circuito contém um indutor e um capacitor e os valores da reatância indutiva e capacitiva são iguais, diz-se que o circuito está em ressonância (X_L = X_C). Como o valor de X_L e X_C são ambos dependentes da frequência, pode-se ver que a ressonância sempre ocorrerá em uma frequência fixa dependente dos valores de impedância e capacitância.

Impedância

No circuito mostrado na FIG. 2.8, a oposição ao fluxo de corrente se deve não apenas à resistência, mas também à reatância indutiva e a reatância capacitiva. Essa oposição total é chamada de impedância (Z). Se a resistência, reatância indutiva e reatância capacitiva são desenhadas vetorialmente com magnitude e direção e com uma linha horizontal representando o ângulo de fase zero, então a resistência será desenhada como uma linha horizontal cujo comprimento é proporcional à sua magnitude. Como uma indutância causa um atraso de fase de 90°, a reatância indutiva pode ser traçada como uma linha vertical para cima cujo comprimento é proporcional à sua magnitude. Da mesma forma, como uma capacitância causa um avanço de fase de 90°, a reatância da capacitância pode ser desenhada como uma linha vertical para baixo, conforme mostrado na FIG 2.9.

Uma representação simplificada das 3 partes componentes de um circuito alternado é mostrada na FIG. 2.10.. A reatância indutiva e a reatância capacitiva estão em oposição uma à outra. A reatância total em Ohms é X_C-X_L. Quando o efeito de Resistência é combinado com a reatância, a oposição total tem um valor vetorial (Amplitude e Ângulo de fase) e torna-se Impedância (Z).

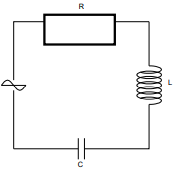
FIGO. 2.8. Circuito Completo (Resistência, indutância, capacitância).

Triângulo de Impedâncias

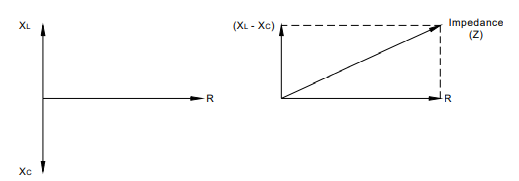
FIGO. 2.9. Triângulo de impedância.
FIG. 2.9. Impedance triangle.

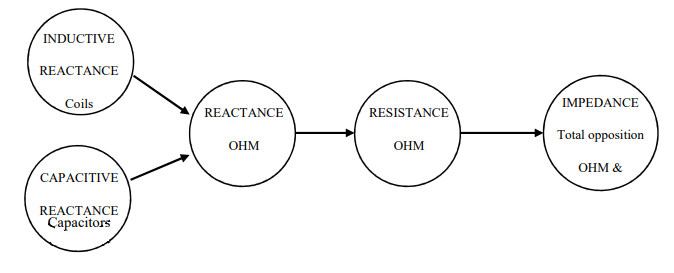
FIGO. 2.10. Relações de impedância.

A impedância e o ângulo de fase da corrente causado pela tensão aplicada à impedância podem ser calculados usando cálculos do triângulo de ângulo reto (Pitágoras). A amplitude da impedância pode ser determinada usando a fórmula:

Fórmula 2.10

Onde
Z = impedância
R = resistência
X_C = reatância capacitiva
X_L = reatância indutiva

Da mesma forma, o ângulo de fase pode ser determinado usando trigonometria com a fórmula:

Ângulo de fase da impedância

Onde
θ° = ângulo de fase
X_C = reatância capacitiva
X_L = reatância indutiva
R = resistência

Como tanto a reatância indutiva quanto a reatância capacitiva variam com a frequência, qualquer variação na frequência mudará a impedância e o ângulo de fase.

Se X_L for maior que X_C, então a impedância Z tem um ângulo de fase atrasado e o circuito é indutivo.
Se X_C for maior que X_L, então a impedância Z tem um ângulo de fase adiantado e o circuito é capacitivo.
Se X_L = X_C, então o ângulo de fase é zero. Então Z = R e o circuito é apenas resistivo

2.2. Magnetismo

O magnetismo é uma propriedade possuída por determinado material pelo qual este material pode exercer uma força mecânica de atração e repulsão em outros materiais semelhantes. O exemplo mais conhecido dos efeitos do magnetismo é a atração que o ímã exerce sobre um prego de ferro.

Materiais magnéticos

Se um objeto é colocado em um campo magnético, uma força é exercida sobre ele e ele fica magnetizado. A intensidade da magnetização depende da suscetibilidade do metal em se magnetizar. Alguns metais são atraídos por um ímã, estes são metais paramagnéticos dos quais os materiais ferromagnéticos são um subgrupo. Outros são repelidos por ímãs; estes são metais diamagnéticos. Uma ilustração dessas relações é mostrada na FIG. 2.11.

Materiais paramagnéticos

Os metais paramagnéticos têm uma suscetibilidade positiva à magnetização, o que significa que são atraídos por ímãs. Alguns são apenas fracamente atraídos; magnésio, molibdênio, lítio e tântalo são exemplos.

Materiais quanto ao magnetismo

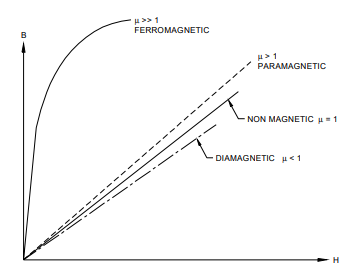
FIGO. 2.11. Relações de permeabilidade ferro-, para-, dia- e não magnéticos.

Metais ferromagnéticos

São materiais paramagnéticos que possuem uma grande e positiva suscetibilidade à magnetização. Eles têm uma forte atração e são capazes de reter sua magnetização após a remoção do campo de magnetização. Ferro, cobalto e níquel são exemplos de metais ferromagnéticos.

Os materiais ferromagnéticos são metais comumente inspecionados com o ensaio de partículas magnéticas. Isso inclui estruturas soldadas de aço e palhetas de turbina a jato à base de níquel.

Materiais diamagnéticos

Os metais diamagnéticos têm uma suscetibilidade pequena e negativa à magnetização ou são levemente repelidos por ímãs. Cobre, prata e ouro são exemplos de materiais diamagnéticos.

2.2.1 Teoria magnética

Um corpo que atrai pequenos pedaços de ferro e aponta na direção norte-sul quando suspenso livremente é chamado de ímã. A extremidade de um ímã apontando para o norte é chamada de polo norte, enquanto a outra é chamada de polo sul. Pólos iguais de dois ímãs se repelem, enquanto pólos diferentes se atraem. O magnetismo do ímã está concentrado nos pólos do ímã. Os dois pólos de um ímã não podem ser separados um do outro. Se um ímã é quebrado em dois pedaços, dois novos ímãs são obtidos. Cada novo ímã tem os pólos norte e sul. Este processo pode ser repetido muitas vezes conforme desejado, mas cada vez é obtido um ímã com ambos os pólos.

Indução e campo magnético

Um campo magnético, como um campo elétrico, pode ser representado por linhas chamadas linhas de indução, cuja direção em cada ponto é a do vetor de indução magnética. O número de linhas de indução por unidade de área normal à direção do campo magnético é chamado de indução magnética e é denotado pela letra B. A unidade de indução no sistema MKS é Weber por metro quadrado (Wb/m²) onde um Weber é igual a uma linha de indução. Da mesma forma, no sistema CGS, a unidade de indução é Maxwell por centímetro quadrado onde um Maxwell é igual a uma linha de indução. Weber/m² é chamado de Tesla (T) e Maxwell/cm² é chamado de Gauss.

Em um campo magnético uniforme, onde o vetor de indução magnética tem uma magnitude constante, as linhas são retas e igualmente espaçadas. Se os pólos de um eletroímã são grandes e próximos, existe uma região entre os pólos onde o campo magnético é aproximadamente uniforme. O número total de linhas de indução passando por uma superfície é chamado de fluxo magnético através da superfície e é denotado por φ. Em um caso especial onde B é uniforme e normal a uma área finita A,

φ = B . A (2.12)

Onde
φ = fluxo magnético na superfície
B = densidade de fluxo
A = área da seção transversal considerada para o cálculo

Como B está em Wb/m² e A está em m², o fluxo está em Webers. Como a indução B em um ponto é igual ao fluxo por unidade de área, ela é frequentemente chamada de densidade de fluxo.

Os maiores valores de indução magnética que podem ser produzidos em laboratório são da ordem de 10 Wb/m² ou 10⁵ Gauss (1 Weber/m² = 10⁴ Gauss), enquanto no campo magnético da Terra a indução é de apenas alguns centésimos de milésimos de Weber por metro quadrado ou alguns décimos de Gauss.

O campo magnético é descrito como a área ao redor de um ímã e pode ser mostrado desenhando linhas imaginárias de força para indicar o caminho que um pólo N isolado percorreria se estivesse livre para se mover. O quão perto as linhas são desenhadas depende da intensidade do campo. As linhas de campo em torno de um ímã na forma de barra são mostradas na FIG. 2.12.

Campo magnético de um imã

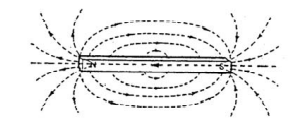
FIG. 2.12. Campos magnéticos do ímã na forma de barra.

Permeabilidade Magnética

A permeabilidade magnética é uma propriedade intrínseca de um material. É a capacidade de um material de concentrar linhas magnéticas. É denotado pela letra grega µ. Qualquer material que seja facilmente magnetizado, como ferro macio (baixo carbono), concentra o fluxo magnético. Esta é a principal característica que separa materiais magnéticos de materiais não magnéticos. A permeabilidade magnética é igual à densidade de fluxo magnético induzido B dividida pela intensidade do campo magnético externo (força de magnetização) H. ou seja

µ = B / H (2.13)

onde
µ = permeabilidade magnética (tesla.metro / ampéres)
B = densidade de fluxo (tesla)
H = força de magnétização (ampéres/metro)

Para ar, vácuo e materiais não magnéticos, µ é constante. Para ar e vácuo, o valor de µ é dado como µo = 4π × 10^-7 Webers/ampere-metro. Os valores numéricos de µ para diferentes materiais são atribuídos em comparação com ar ou vácuo. Isso é chamado de permeabilidade relativa e é definido como

µ_r = µ / µ_o (2.14)

onde
µ_r = permeabilidade relatíva (adimensional)
µ = permeabilidade (absoluta)
µ_o = permeabilidade do vácuo

O µ_r é uma quantidade adimensional porque é uma razão comparando duas densidades de fluxo. Como o ar, o vácuo e qualquer outro material não magnético não podem afetar um campo magnético por indução, todos eles têm µ_r igual a 1. Para materiais magnéticos, µ_r pode ser muito grande. Os valores típicos para o ferro são de 100 a 5.000.

Outra permeabilidade preocupante no ensaio de correntes parasitas é a permeabilidade incremental ou de auto-bobina, ∆µ. É definido como

∆µ =∆B / ∆H (2.15)

Magnetização do ferro

Materiais como aço macio (N.T. Também conhecido como aço doce ou de baixo carbono) que são facilmente magnetizáveis, perdem parte ou todo o magnetismo na remoção do campo aplicado. Os domínios magnéticos que se alinham com o campo aplicado são assim facilmente perturbados na remoção do campo externo deixando o material parcialmente magnetizado. O fluxo pode existir nos materiais mesmo na ausência de força de magnetização externa, como em ímãs permanentes. A amostra magnética na forma de anel com um enrolamento toroidal pode ser magnetizada a partir de seu estado original não magnetizado. O gráfico dos respectivos valores de densidade de fluxo B e intensidade de magnetização H é conhecido como curva de magnetização. Exemplos dessas curvas são dados nas Figuras 2.13. (a) e (b). A linha de base horizontal, ou eixo X é marcada em unidades de força de magnetização H, em Oersteds. A linha de resposta vertical, ou eixo Y indica densidade de fluxo B em Gauss. Sua forma varia de um tipo de material para outro devido à sua permeabilidade magnética.

À medida que a força de magnetização H é aplicada ao ferro, as paredes dos domínios se movem de modo a favorecer o crescimento dos domínios que têm sua direção de magnetização mais ou menos ao longo da direção do campo externo. À medida que o campo é aumentado, as forças são grandes o suficiente para causar a rotação gradual da direção da magnetização em alinhamento exato com o campo. Finalmente, quando todos os dipolos estão alinhados, B atingiu um valor constante ou está saturado.

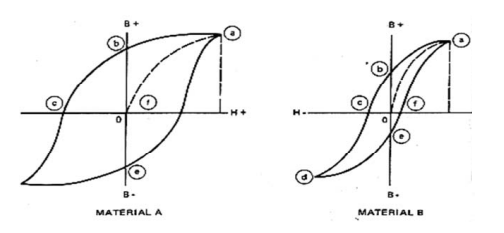
Curva de histerese de material duro e macio

Curva de histerese de material duro e macio

FIG. 2.13. Curva de histerese para materiais duros (a) e macios (b).

Se o campo for removido após a amostra ser magnetizada, o material tende a retornar ao seu estado não magnetizado. Mas o movimento das paredes do domínio é parcialmente inibido pelos limites do cristal e suas imperfeições cristalinas. Isso produz um tipo de atrito que faz com que as paredes fiquem para trás da posição que teriam se se movessem facilmente dentro da amostra. Isso significa que os dipolos magnéticos não são perfeitamente elásticos e não retornam à sua posição original quando a força externa é removida.

A partir das curvas mostradas na FIG. 2.13. para ferros macios e duros é evidente que a permeabilidade não é constante e é dada pela razão de B para H, que pode ser encontrada em qualquer ponto anotando os respectivos valores.

2.2.2 Fluxo magnético induzido

Definição

O número total de linhas de indução passando por uma superfície é chamado de fluxo magnético. É denotado por φ. O fluxo magnético pode ser induzido em um condutor colocando-o no campo de um ímã permanente ou de um eletroímã.

Linhas de força e campos de força

O espaço ao redor de um ímã onde a influência do ímã é sentida por outro ímã ou um material magnético é chamado de campo magnético. O campo magnético é representado por linhas de campo magnético (ou linhas de força magnética). O caminho ao longo do qual um pólo norte isolado de um ímã se move no campo magnético é chamado de linha de campo. As linhas de campo são direcionadas do pólo N do ímã para o pólo S. As linhas de campo não se cruzam.

O campo magnético em uma amostra de teste pode ser criado pela passagem de correntes diretamente na amostra ou de maneira indireta, por meio da qual o campo é criado na amostra ferromagnética por indução. A amostra é magnetizada desta forma, colocando-a axialmente na bobina pré-enrolada, solenóide ou colocando-a ao redor do condutor que transporta a corrente. As linhas de força como resultado do campo aplicado seriam circulares ou longitudinais.

Conservação de fluxo e magnetismo residual

Quando um material ferromagnético não magnetizado é submetido a uma força de magnetização externa, o comportamento ou resposta à intensidade magnética e fluxo resultante é como mostrado na curva de magnetização da FIG. 2.13. Se o campo de magnetização for forte o suficiente, o processo gradual de alinhamento dos domínios continua até que todos os domínios estejam alinhados e o corpo de prova esteja saturado. O comportamento do material ferromagnético sob o ciclo completo de magnetização é complexo e notamos que a densidade de fluxo B não retorna a zero, pois quando o valor de H se torna zero ainda há magnetismo residual, também chamado de remanência, igual ao valor de '0b ' da curva na FIG. 2.13.

Se o sentido da corrente de magnetização é invertida e gradualmente aumentada em valor, o campo magnetico irá se reduzir até que a densidade de fluxo chegue a zero no ponto (c), e o valor '0c' é a força coerciva, campo negativo necessário para desmagnetizar a amostra. Continuando a aumentar a corrente de magnetização inversa fará com que o material atinja a saturação na direção oposta no ponto (d). Se a corrente de magnetização é agora diminuida a zero, o campo residual do ponto (e) se encontra na direção oposta ao do ponto (b). Posterior aumento da corrente de magnetização (agora na direção H+) reduz o campo magnético a zero no ponto (f). Continuando a crescer a força de magnetização H o material atingirá a saturação no ponto a fechando o ciclo que é conhecido como curva de histerese.

2.2.3 Lei de Ohm Magnética

A lei de Ohm no magnetismo é análoga à lei de Ohm na eletricidade. Ele afirma que 'A Força Magnetomotriz (FMM) é diretamente proporcional ao fluxo magnético (ф) produzido por esta força.'

Matematicamente, pode se escrever como

MMF ∝ ф
or
MMF = фR
ou
ф = MMF / R (2.16)

onde
ф = fluxo magnético
MMF = força magnetomotriz
R = resistência magnética

Força magnetomotriz

A força que produz o campo magnético é chamada de força magnetomotriz (FMM). Em um circuito elétrico, uma FEM conduz uma corrente através do condutor. No magnetismo, a força magnetomotriz (FMM) produz o fluxo que flui através das linhas de fluxo. Maior a corrente elétrica, mais forte o campo elétrico, e no caso de uma bobina, maior o número de voltas, mais concentrado é o campo. Portanto, o FMM é dada como

MMF = N . I (2.17)

onde:
FMM = força magnetomotiva
N = numeros de espiras da bobina
I = corrente em Amperes

A unidade de FMMF no SI é Ampere-espira. No sistema CGS a unidade de FMM é Gilbert, abreviada como Gb. 1 Ampere-volta = 4π/10 Gilbert (= 1,26 Gilbert).

Relutância

A relutância no circuito magnético é comparável à resistência no circuito elétrico. É definida como a oposição ao estabelecimento de fluxo magnético no material sob a influência do campo magnetizante.

O material com alta permeabilidade tem baixa relutância e vice-versa. A relutância do material determina a magnitude do fluxo produzido pelo FMM como dado pela lei de Ohm magnética.

Circuitos Magneticos

As linhas de fluxo magnético formam laços fechados. Se todo o fluxo magnético (ou substancialmente todo ele) associado a uma distribuição particular de correntes está confinado a um caminho bem definido, então podemos falar de um circuito magnético. Um toróide é um exemplo de circuito magnético, pois o fluxo magnético está confinado à região dentro do enrolamento toroidal.

O circuito magnético é análogo ao circuito de corrente e, devido a essa analogia, as combinações de relutância em série e em paralelo podem ser combinadas da mesma maneira que as combinações de resistência em série e em paralelo.

A relutância R é inversamente proporcional à permeabilidade µ. Uma vez que a permeabilidade do material ferromagnético pode ser 100 vezes µ_o, 10³ µ_o ou mesmo 10⁵ µ_oem certas circunstâncias, é aparente que o material ferromagnético forma um caminho de baixa relutância para o fluxo magnético. Se o fluxo magnético encontrar dois caminhos paralelos, um de alta relutância R_h e outro de baixa relutância R_l , então a maior parte do fluxo passará pelo caminho de baixa relutância, e a relutância equivalente da combinação é dada por

Cálculo da relutância

Onde
R = relutância
R_h = alta relutância
R_l = baixa relutância

2.3. Campo magnético produzido por uma corrente

As primeiras observações registradas de campos magnéticos criados por correntes foram as de Oersted, que descobriu que uma agulha de bússola pivotada, próxima a um fio no qual havia uma corrente, se posicionava com seu longo eixo perpendicular ao fio . Experimentos posteriores de Biot e Savart, e de Ampere, levaram a uma relação por meio da qual podemos calcular a densidade de fluxo em qualquer ponto do espaço ao redor de um circuito no qual existe uma corrente.

2.3.1 Lei de Biot e Savart

Definição

O campo magnético envolve o condutor de corrente. Para um condutor reto longo carregando uma corrente unidirecional, as linhas de fluxo magnético são caminhos circulares fechados concêntricos com o eixo do condutor. Biot e Savart deduziram, a partir do estudo experimental do campo em torno de um longo condutor reto, que a densidade de fluxo magnético B associada ao condutor de corrente infinitamente longa em um ponto P que está a uma distância radial r, como ilustrado na FIG. 2.14, é

Cálculo deB

Onde
B = densidade de fluxo magnético
µ = permeabilidade do espaço livre
I = corrente
r = distância radial

Ao contrário do campo elétrico em torno de um fio carregado, que é radial, as linhas de indução magnética são círculos concêntricos ao fio e dispostos em planos perpendiculares a ele. A direção desse circuito fechado concêntrico de linhas magnéticas é dada pela regra da mão direita.

Campo magnético de um fio

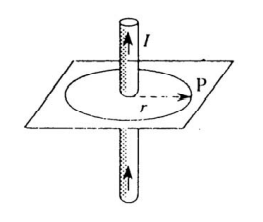
FIG. 2.14. Campo magnético em torno de um condutor de corrente longo e reto.

Regras práticas
Considere um condutor através do qual a corrente I está fluindo verticalmente para cima, como mostrado na FIG. 2.14. Suponha que queremos encontrar a densidade de fluxo magnético devido a este condutor de corrente em um ponto P cuja distância perpendicular ao condutor é r. Foi encontrado experimentalmente por Biot e Savart que em qualquer ponto:

(a) a densidade do fluxo magnético é diretamente proporcional à corrente. ou seja, B ∝ I.
(b) a densidade de fluxo magnético é diretamente proporcional ao comprimento efetivo do condutor, ou seja, B ∝ l.
(c) a densidade de fluxo magnético é inversamente proporcional a distância r do ponto P ao condutor, ou seja, B ∝ 1/r² .

Regra da mão direita

As linhas de indução magnética são círculos concêntricos com o fio e situados em planos perpendiculares a ele. A direção desse circuito fechado concêntrico de linhas magnéticas é dada pela regra da mão direita, que afirma: “Se o condutor for agarrado pela mão direita com o polegar apontando na direção da corrente, os dedos curvados da mão apontarão a direção do campo magnético", como mostrado na FIG. 2.15.

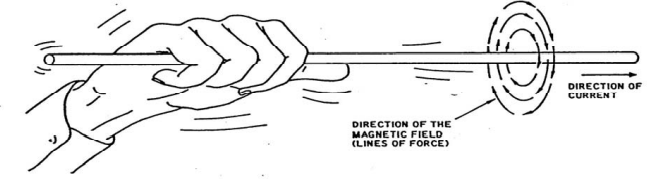
FIG. 2.15. Regra da mão direita de Fleming.

2.3.2 Lei de Ampere

Definição

A lei de Ampere afirma que “a densidade de fluxo magnético sobre uma superfície fechada é diretamente proporcional à corrente contida pela superfície”.

A equação 2.19 pode ser escrita como 2πrB = µ_oI. Isso mostra que o produto de 2πr e B é igual a µ_oI. Mas 2πr é o comprimento do caminho ao redor do condutor e nele o valor de B é o mesmo em todos os pontos. Ampere generalizou esse resultado em uma lei. Matematicamente, pode ser escrito como

B . l = µ_o . I

onde
B = densidade de fluxo magnético
l = comprimento
µ_o = permeabilidade do espaço livre
I = corrente

Esta lei é aplicável a caminhos fechados que não sejam circulares.

Assim, a lei de Ampère também pode ser definida como “O produto escalar de B e l em torno de qualquer caminho fechado é igual a µ_oI, onde I é a corrente total constante que passa pelo caminho”.

O caminho é dividido em vários elementos de pequeno comprimento como mostrado na FIG. 2.16. Considere um elemento de comprimento dl do caminho fechado. De acordo com a lei de Ampere, pode ser escrito como

Formula 2.21

onde
dl = variação do comprimento
B = densidade de fluxo magnético
µ_o = permeabilidade do espaço livre
I = corrente

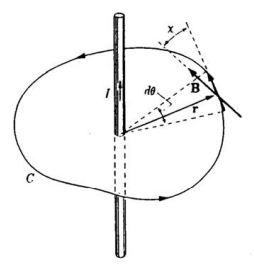
FIG. 2.16. Verificação da lei de Ampere para geometria de condutores retos longos.

Aplicações

(a) Campo devido à corrente em um toróide

Um toróide é um solenóide que foi obtido por sua conformação (dobramento do seu eixo) em um círculo. Considere um toróide de raio r, com N espiras e corrente I fluindo através dele. Quando a corrente passa por cada espira, linhas magnéticas circulares de força passam pelas espiras do toróide.

Aplicando a lei de Ampere ao longo do eixo do toróide, podemos escrever

∫B . dl = µ_o × (corrente contida) = µ_o NI

Como o ângulo entre B e dl é zero e ∫dl = 2πr, portanto, o campo magnético devido à corrente em um toróide de acordo com a lei de Ampere é dado por

Formula 2.22

onde
B = densidade de fluxo magnético
µ_o = permeabilidade do espaço livre
I = corrente
r = distância radial

O campo magnético não é uniforme ao longo de uma seção transversal do núcleo, porque o comprimento do caminho l é maior na parte externa da seção do que no lado interno. No entanto, se a espessura radial do núcleo for pequena em comparação com o raio do toróide r, o campo varia apenas ligeiramente ao longo de uma seção. Neste caso, considerando que 2πr é o comprimento da circunferência do toróide e que n = N/ 2πr é o número de voltas por unidade de comprimento, o campo pode ser escrito como

B = µ_onI (2.23)

onde
B = densidade de fluxo magnético
µ_o = permeabilidade do espaço livre
n = número de voltas/unidade de comprimento
I = corrente

As equações derivadas acima para o campo em um solenóide ou toróide estreitamente enrolado são estritamente corretas apenas para um enrolamento no vácuo. Para a maioria dos propósitos práticos, no entanto, eles podem ser usados para um enrolamento no ar ou com núcleo de material não ferromagnético.

(b) Campo devido à corrente em uma bobina

Uma bobina é construída enrolando um fio na forma helicoildal em torno de uma superfície cilíndrica. As espiras do enrolamento são normalmente espaçadas e podem consistir em uma ou mais camadas. Quando está conectado a uma bateria, uma corrente elétrica flui através de cada volta e produz um campo magnético. Este campo magnético é bastante uniforme e mais forte dentro das espiras, mas é mais fraco e insignificante fora da bobina.

Para saber o valor do campo magnético da bobina aplicamos a lei de Ampere. O campo fora da bobina é zero e o campo dentro da bobina é uniforme e mais forte e está ao longo do eixo da bobina. Portanto, pela lei de Ampere

∫ B . dl = µ_oI

O valor de B serão os mesmos que o caso de um toroide, isto é

B = µ_onI

A direção de B é ao longo do eixo da bobina.

2.4. Lei da indução eletromagnética

A tensão induzida é o resultado de um fluxo magnético cortando um condutor, produzido pelo movimento físico do campo magnético ou do condutor. Quando a corrente em um condutor varia em amplitude, no entanto, as variações de corrente e seu campo magnético associado são equivalentes ao movimento do fluxo. À medida que a corrente aumenta de valor, o campo magnético se expande para fora do condutor. Quando a corrente diminui, o campo colapsa no condutor. À medida que o campo se expande e colapsa com as mudanças de corrente, o fluxo está efetivamente em movimento. Portanto, uma corrente variável pode produzir tensão induzida sem a necessidade de movimento do condutor.

O resultado de um campo de fluxo em expansão e em colapso é o mesmo que o de um campo em movimento. Esse fluxo em movimento corta o condutor que fornece a corrente, produzindo tensão induzida no próprio fio. Além disso, qualquer outro condutor no campo, transportando corrente ou não, também é cortado pelo fluxo variável e possui tensão induzida.

2.4.1 Lei de Lenz

Definição
A lei de Lenz afirma: “A direção de uma corrente induzida é tal que se opõe à causa que a produz”.

A 'causa' da corrente pode ser o movimento de um condutor em um campo magnético, ou pode ser a mudança de fluxo através de um circuito estacionário. No primeiro caso, a direção da corrente induzida no condutor em movimento é tal que a direção do empuxo lateral exercido sobre o condutor pelo campo magnético é oposta em direção ao seu movimento. O movimento do condutor é, portanto, 'oposto'.

No segundo caso, a corrente cria um campo magnético próprio, que dentro da área delimitada pelo circuito é oposto ao campo original se este estiver aumentando, mas no mesmo sentido do campo original se este estiver diminuindo . Assim, é a mudança no fluxo através do circuito (não o fluxo em si), que é 'oposta' pela corrente induzida.

Fator de auto-indução

A capacidade de um condutor de induzir tensão em si mesmo quando a corrente muda, é chamada de auto-indutância ou auto-indutância ou simplesmente indutância. O símbolo da indutância é L e sua unidade é o Henry. Um Henry é a quantidade de indutância que permite que um Volt seja induzido quando a corrente muda à taxa de um Ampere por segundo. O fator de auto-indução é dado por

Cálculo da indutância

onde
L = indutância
E_ind = voltagem induzida
∆I = variação da corrente
T = tempo

O sinal negativo para E indica que a polaridade da tensão induzida está em oposição à mudança de corrente, mas a polaridade pode ser desconsiderada no cálculo do valor de L.

A indutância de uma bobina aumenta com o número de voltas, diâmetro da bobina, e a permeabilidade do núcleo. Para uma bobina de núcleo de ar e reta, a indutância aumenta com o quadrado das voltas e do diâmetro. Dobrar as voltas fornece quatro vezes a indutância e dobrar o diâmetro fornece quatro vezes a indutância. Se o número de voltas e o diâmetro forem duplicados, a indutância é aumentada por um fator de 16. A indutância também aumenta diretamente com o comprimento, ou seja, dobrar o comprimento fornece o dobro da indutância.

Fator de indutância mútua

Quando a corrente em um indutor muda, o fluxo variável pode cortar qualquer outro indutor próximo, produzindo tensão induzida em ambos os indutores. Considere duas bobinas L1 e L2 colocadas próximas uma da outra. A bobina L1 é conectada a um gerador CA. O enrolamento L2 não está ligado a L1, mas as espiras estão ligadas pelo campo magnético. Variar a corrente em L1 induz tensão em L1 e em L2. Se todo o fluxo de corrente em L1 influenciar todas as espiras da bobina L2, cada espira em L2 terá a mesma quantidade de tensão induzida que cada espira em L1. Além disso, quando a tensão induzida produz corrente em L2, seu campo magnético variável induz tensão em L1. As duas bobinas têm indutância mútua porque a corrente em uma bobina pode induzir tensão na outra. A indutância mútua das duas bobinas (M) pode ser escrita como

M = ( L₁ L₂ )^1/2 (2.25)

onde
M = indutância mútua
L₁ = indutância da bobina 1
L₂ = indutância da bobina 2

Fator de acoplamento

A fração do fluxo total de uma bobina influenciado outra bobina é o coeficiente de acoplamento. É indicado pela letra k. O coeficiente aumenta colocando a bobina sensora perto do condutor ensaiado. Quando sonda de correntes parasitas são usadas, o espaçamento entre a bobina e o material condutor ensaiado é chamado de lift-off. Quando são usadas bobinas envolventes ou internas, o acoplamento é chamado de fator de enchimento. O coeficiente de acoplamento é aumentado colocando a bobina próxima ao material condutor ensaiado. Um valor mais alto de k, chamado acoplamento justo (no inglês, 'tight'), permite uma melhor indução mútua. O acoplamento frouxo (no inglês, 'loose'), com um valor baixo de k, tem o efeito oposto.

2.4.2 Correntes induzidas

Corrente induzida em uma bobina em curto-circuito

A lei de Faraday afirma que sempre que um campo magnético corta um condutor, uma corrente elétrica fluirá no condutor se for fornecido um caminho fechado sobre o qual a corrente possa circular. A corrente alternada que flui através da bobina de ensaio produzirá um campo magnético variável na bobina. Se qualquer outra bobina for colocada no campo magnético da bobina, uma corrente na segunda bobina será induzida. Se a bobina for colocada muito perto da bobina de excitação, a quantidade de corrente induzida na outra bobina pode ser a mesma que flui através da bobina de excitação.

Corrente induzida em uma massa metálica

A corrente alternada que flui através da bobina de ensaio produz um campo magnético alternado na bobina. Quando a bobina de ensaio é aproximada ou colocada sobre o condutor metálico, o campo magnético passa (corta) no material e correntes circulares (eddy) são induzidas no material como mostrado na FIG. 2.17.

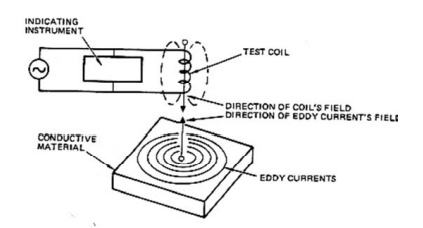
Esquema básico do aparelho de correntes parasitas

Esquema básico do aparelho de correntes parasitas

FIG. 2.17. Equipamento básico do ensaio de correntes parasitas.

A corrente no condutor (corrente parasita) irá gerar um campo magnético secundário, que induz uma corrente na bobina sensora. Essa indutância mútua causa uma mudança na impedância da bobina. Os sinais de impedância detectados pela bobina sensora são as medições do corpo de prova. Assim, a técnica de correntes parasitas utiliza o efeito de campos eletromagnéticos e indução para caracterizar propriedades físicas de materiais metálicos.

Efeito de pele

As correntes parasitas induzidas por um campo magnético variável concentram-se perto da superfície adjacente à bobina de excitação. As correntes parasitas que fluem no objeto de ensaio em qualquer profundidade produzem campos magnéticos que se opõem ao campo primário, reduzindo assim o fluxo magnético líquido e causando uma diminuição no fluxo de corrente à medida que a profundidade aumenta.

Alternativamente, correntes parasitas próximas à superfície podem ser vistas como blindagem do campo magnético da bobina, enfraquecendo assim o campo magnético em maiores profundidades e reduzindo as correntes induzidas. Esse fenômeno é conhecido como efeito de pele.

Campo criado por correntes parasitas

Em uma bobina de ensaio, o fluxo magnético ф_p é obtido passando a corrente alternada através dela. Quando esta bobina é aproximada da amostra condutora, correntes parasitas são induzidas na amostra. As correntes induzidas têm seu próprio fluxo magnético associado a elas. A direção do fluxo magnético ф_s asassociado às correntes induzidas é tal que se opõe ao fluxo magnético da bobina ф_p (lei de Lenz), diminuindo assim o fluxo magnético líquido. Isso resulta em mudança de impedância da bobina e queda de tensão. FIG. 2.18. ilustra a direção dos fluxos primário e secundário.

É a oposição entre o campo primário e secundário (correntes parasitas) que fornece a base para a extração de informações durante o ensaio de correntes parasitas. Deve-se notar que se a amostra for ferromagnética, o fluxo magnético é reforçado apesar dos efeitos opostos das correntes parasitas. A alta permeabilidade dos materiais ferromagnéticos os distingue dos materiais não ferromagnéticos e influencia fortemente os parâmetros de teste de correntes parasitas.

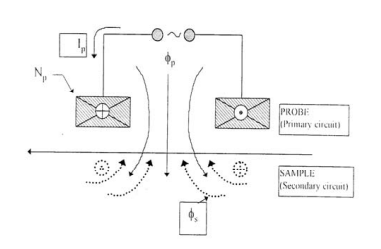
FIG. 2.18. Campo gerado pelas correntes parasitas.

Reatância

O fluxo magnético líquido da bobina diminui à medida que seu campo intercepta um material condutor não magnético. Isso reduz a indutância da bobina de excitação e sua reatância indutiva. A magnitude dessa redução depende do seguinte:

condutividade dos materiais de teste
frequência de teste
proximidade da bobina de magnetização ao material ensaiado.

A reatância da bobina de teste nas proximidades do material ferromagnético, por outro lado, aumenta à medida que o material altamente permeável é colocado no campo da bobina de excitação. Isso acontece porque essas linhas de fluxo que entram na peça de teste ferromagnética encontram parte de seu caminho no material que tem muito menos relutância do que o ar. O campo de excitação inclui então densidades de fluxo aumentadas que são circundadas pelos enrolamentos da bobina.

2.5. Fatores que afetam as correntes parasitas

2.5.1 Introdução

Os fatores que afetam as correntes parasitas são:

(a) Condutividade σ (Sigma)
(b) Permeabilidade µ (mu)
(c) Frequência f
(d) Proximidade (lift off/fator de enchimento)
(e) Geometria
(f) Manuseio da Sonda
(g) Descontinuidades (Defeitos)

Devido ao grande número de variáveis na inspeção por correntes parasitas, para corretamente interpretar as causas do surgimento de uma indicação, todas os sete (7) fatores citados acima devem ser considerados.

2.5.2 Considerações práticas

Condutividade

Enquanto a condutividade elétrica do material é a mesma, existem fatores internos que podem implicar em mudanças na condutividade aparente local, quais sejam

(a) Composição química da liga metálica.
Ligas metálicas são combinações químicas de outros metais e/ou elementos quimicos com o metal base da liga. Cada metal ou elemento químico tem um efeto individual na condutividade do metal de base. A condutividade do metal de base é modificada para um valor relacionado a composição química da liga metálica. Dessa forma é possível identificar metais puros e suas ligas pela medição da condutividade.
(b) Dureza.
Quando um metal ou liga é sujeito a um tratamento térmico (ou a aquecimento escessivo durante sua operação normal) o metal ficará endurecido ou macio dependendo do material. Essa mudança de dureza ocorre devido a mudanças microestruturais internas que afetarão a acondutividade do mateial. Essa mudança na condutividade pode também ser detectada por métodos do ensaio de correntes parasitas. Tratamento térmicos aplicados indevidamente também podem ser detectados dessa forma.
(c) Temperatura e Tensões Residuais.
A temperatur ambiente e tensões residuais internas do material ensaiado também tem um efeito na condutividade do material. Essas mudanças podem também ser detectas pelo ensaio de correntes parasitas. Um aumento na temperatura do material normalmente resulta na diminuição da condutividade do material. Tensões residuais provocam uma mudança imprevista, mas detectavel na condutividade.
(d) Revestimentos Condutores.
A presença de revestimentos condutores sobre materiais de base também condutores mudam a condutividade aparente do metal de base assim como o efeito de adição de elementos de liga. Entretanto, se a espessura desse revestimento varia, a condutividade aparente também irá variar. Essa mudança de espessua pode ser detectada pelo ensaio de correntes parasitas.

Permeabilidade

Quando uma bobina de teste energizada é colocada sobre um material ferromagnético não magnetizado, o campo é muito intensificado pelas propriedades magnéticas do material, de modo que ocorre uma grande mudança na impedância da bobina de teste.

Se a intensidade do campo magnético em vários locais variar um pouco, essas pequenas variações terão um grande efeito na impedância da bobina. Essas mudanças na impedância da bobina são muitas vezes tão grandes (em comparação com as mudanças causadas por mudanças na condutividade ou dimensão) que mascaram todas as outras mudanças. Quando a geometria da amostra permite, esse efeito pode ser superado pela magnetização do material até a saturação usando uma bobina separada alimentada por corrente contínua. A saturação magnética elimina efetivamente quaisquer variações no campo magnético residual devido a variáveis magnéticas e, assim, permite que outras variações sejam medidas. Após a conclusão do ensaio, a peça deve ser desmagnetizado.

Frequência

A frequência é uma das poucas variáveis controladas pelo inspetor no ensaio de correntes parasitas. O principal uso da frequência é controlar a profundidade de penetração, densidade e fase das correntes parasitas induzidas. Em termos gerais, frequências mais altas são usadas para detectar descontinuidades superficiais e frequências mais baixas para ensaios subsuperfíciais.

Proximidade sonda-peça (acoplamento eletromagnético)

Lift off (sem tradução em português) e fill factor (fator de enchimento) são termos para descrever qualquer espaçamento que ocorra entre a peça ensaiada e a bobina de inspeção. Cada um desses termos têm efeito identico nas correntes parasitas. Lift off e fill factor exercem essencialmente o mesmo efeito no ensaio, embora o primeiro seja aplicado a sondas superficiais e o outro a sondas circulares (internas ou envolventes).

(a) Lift Off. Quando uma sonda superficial é energizada e deixada no ar acima de um material condutor a impedância da bobina possui um certo valor. Quado a sonda é aproxiamada do condutor esse valor inicial muda quando as linhas de força do campo magnético da bobina interceptam o material condutor. Porque o campo da bobina é mais forte nas proximidades da bobina, a impedância da bobina continuará a se modificar até que a sonda toque o material. Outra consequência da influência da distância sonda-peça é que qualquer pequena variação da separação entre a bobina e o material condutor modificará a impedância da bobina. O efeito lift off é tão proeminente que qualquer variação do espaçamento sonda-peça pode vir a mascarar muitas indicações de descontinuidades superficiais.
(b) Fill Factor (fator de enchimento). Em uma sonda envolvente, ou em uma sonda interna, o fator de enchimento é definido como quão bem a sonda interna preenche o espaço da peça, ou quão bem a peça preeche o espaço da sonda envolvente. O cálculo é feito então pela relação entre os diâmetros quadrados dos componentes envolvidos, sendo que o resultado deve ser sempre menor que a unidade. Novamente, qualquer pequena mudança nos diâmetros envolvidos causam uma mudança na impedância da bobina. Esse efeito pode ser útil na medição do diâmetro da peça condutora, mas sua variação pode também mascarar outras indicações superficiais.

Geometria

Os dois principais fatores na geometria do componente que afetam as correntes parasitas são a espessura e o efeito de borda/extremidade.

(a) Espessura. Mudanças na espessura do material pode ser causada pela geometria da peça manufaturada ou por corrosão/erosão em serviço. Se a espessura do material é menor que a profundidade de penetração efetiva, qualquer mudança na espessura do material afetará as correntes parasitas e pode ser utilizada para medir a espessura do material.
(b) Efeito de borda/extremidade. As correntes parasitas são distorcidas na extremidade, ou na aresta da peça quando uma sonda se aproxima dessas regiões porque as correntes não têm caminho para fluir. Os resultados da distorção causada nas correntes parasitas resulta em um indicação falsa conhecida como efeito de borda. Efeito de borda também aparece na interface entre materiais diferentes.

Como, para a bobina de ensaio, a borda da peça se parece com uma trinca ou furo muito grande, há uma reação muito forte que mascarará qualquer alteração devido a outros fatores. O limite de quão perto da borda uma bobina pode ser colocada é determinado pelo tamanho da bobina e qualquer blindagem aplicada.

N.T.: A minimização do efeito de borda no ensaio pode ser tentada mantendo a distânca da sonda a extremidade da peça constante durante a varredura. Varredura paralela a aresta/extremidade.

Manuseio da sonda

Sob condições ideais, a bobina da sonda deve ser escaneada na superfície de ensaio em um ângulo constante em relação à superfície com elevação e pressão constantes. Mudanças no ângulo da sonda, pressão de contato ou na forma como a sonda é segurada (capacitância manual) causarão alterações no sinal do ensaio.

Em ensaios não destrutivos, onde a maioria das inspeções utiliza o método de bobina de contato superfícial manual, a influência de uma técnica de manuseio de sonda ruim não pode ser enfatizada. Os efeitos do manuseio da sonda podem ser reduzidos com o uso de sondas especiais com mola que mantêm a sonda em um ângulo e pressão constantes na superfície. Estes são geralmente usados onde a varredura o deve ser realizada em superfícies planas, ou onde as medições de condutividade ou espessura da tinta estão sendo tomadas. Ao escanear próximo a mudanças de seção (efeito de geometria), o uso de guias simples ajudará no bom manuseio da sonda, resultando em uma inspeção mais eficaz.

Descontinuidades

As trincas causam uma distorção do campo de correntes parasitas devido ao fato de que as correntes parasitas precisam fluir em torno delas. Isso resulta em um caminho de resistência aumentado e uma redução correspondente na força de correntes parasitas. Da mesma forma, a corrosão causa um aumento da resistência dentro do material com uma redução correspondente na força de correntes parasitas. Em cada caso, resultará uma mudança na exibição do medidor ou do ponto.

Para garantir que as inspeções sejam realizadas em um padrão repetitivo, são usados blocos de referência com defeitos artificiais. Esses blocos devem ser de especificação de material semelhante (liga, tratamento térmico, condutividade) ao componente em teste. Ao configurar o detector de falhas (padronização) para fornecer uma resposta conhecida do defeito artificial, uma inspeção pode ser realizada repetidamente no mesmo padrão.

As configurações de sensibilidade do detector de falhas (padronização) devem ser verificadas, em intervalos regulares e no mínimo.

(a) Antes de cada inspeção.
(b) Após cada inspeção.
(c) Ao obter uma indicação de falha suspeita/antes de confirmar uma indicação de falha.

Nota: Se for descoberto que a configuração do detector de falhas está incorreta, todos os componentes testados desde que a padronização correta anterior foi confirmada, devem ser testados novamente.