EC16 - Mostrador - Plano Complexo de Impedância ("eddy scope")

traduzido do sítio: http://www.nde-ed.org/EducationResources/HighSchool/Magnetism/Physics/impedanceplane.php

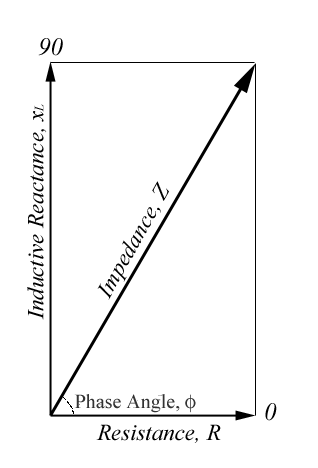
Impedância Elétrica (Z), é a oposição total que um circuito apresenta a uma corrente alternada. A impedância, medida em ohms, pode incluir resistência (R), reação indutiva (X_L)e reatância capacitiva (X_C). Os circuitos dos aparelhos de correntes parasitas geralmente apresentam apenas componentes R e X_L . Como discutido na página sobre impedância, os componentes de resistência e de reatância indutiva não estão em fase, por isso a adição vetorial deve ser usada para calcular a impedância. Para um circuito do aparelho de correntes parasitas com componentes de resistência e de reatância indutiva, a impedância total é calculada usando a equação a seguir.

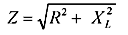
Você se lembra que isso pode ser exibido graficamente usando o gráfico do plano de impedâncias, como visto na figura acima. O vetor impedância também tem um ângulo associado, chamado ângulo de fase, que pode ser calculado pela seguinte equação.

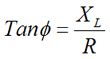
O gráfico do plano de impedância é uma maneira muito útil de exibir os resultado do ensaio de correntes parasitas. Como mostrado na figura abaixo, as grandezas influentes no ensaio de correntes parasitas (condutividade elétrica, permeabilidade magnética, grandezas dimensionais da peça, e acoplamento eletromagnético sonda-peça)  fazem com que o sinal de corrente parasita no plano de impedância reaja (se desloque) de várias maneiras diferentes.

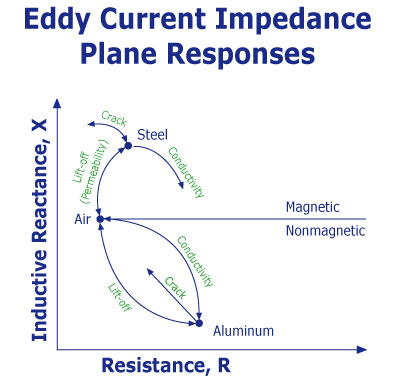
Se o sistema de corrente parasita for balanceado (com a sonda) no ar e depois a sonda colocada (acoplada) em uma peça de alumínio, o componente resistivo do sinal aumentará (porque correntes parasitas estão sendo geradas no alumínio e isso tira energia da bobina, que é mostrada como o aumento da resistência) e a reatância indutiva da bobina diminui (o campo magnético criado pelas correntes parasitas se opõe ao campo magnético da bobina e o efeito líquido é um campo magnético mais fraco para produzir indutância). Se uma trinca estiver presente no material, menos correntes parasitas serão capazes de circular e a resistência voltará a diminuir e a reatância indutiva voltará a subir. Mudanças na condutividade do material ensaiado farão com que o sinal do ensaio seja diferente do sinal de acoplamento a peça de alumínio, anteriormente explicado.

Quando uma sonda é acoplada a um material magnético como o aço, algo diferente acontece. Assim como com o alumínio (condutor, mas não magnético), as correntes parasitas se formam, tirando energia da bobina, que aparece como um aumento da resistência das bobina. E, assim como com o alumínio, as correntes parasitas geram seu próprio campo magnético que se opõe ao campo magnético da bobina. No entanto, você notará no gráfico que a reação aumenta. Isso ocorre porque a permeabilidade magnética do aço concentra o campo magnético da bobina. Esse aumento na força do campo magnético ofusca completamente o campo magnético das correntes parasitas. A presença de uma trinca ou uma mudança na condutividade produzirá uma mudança no sinal de corrente parasita semelhante ao visto com alumínio.

No aplicativo abaixo, as curvas de liftoff podem ser geradas (na tela do aparelho) para diversos materiais não magnéticos com diferentes condutividades elétricas. Com a sonda afastada da superfície metálica, zerar o sistema (balancear) e limpar a tela (gráfico). Em seguida, mova lentamente a sonda para se acoplar a superfície do material. Levante a sonda de volta, selecione um material diferente e contate a sonda de volta à superfície da outra amostra.

Clique aqui para executar um aplicativo JavaScript sobre efeitos da condutividade e do liftoff no plano de impedâncias.

Experiência

Gerar uma família de curvas de liftoff para os diferentes materiais disponíveis no aplicativo usando uma freqüência de 10kHz. Observe a posição relativa de cada uma das curvas. Repita a mesma experiência para as freqüências de 500kHz e 2MHz. (Nota: pode ser útil capturar uma imagem do conjunto completo de curvas para cada freqüência para comparação)

1) Qual freqüência seria melhor se você precisasse distinguir entre dois materiais de alta condutividade?

2) Qual freqüência seria melhor se você precisasse distinguir entre dois materiais de baixa condutividade?

3) Qual o inconveniente que pode surgir no ensaio quando usando a freqüência melhor se você precisasse distinguir entre dois materiais de alta condutividade?

O cálculo da impedância para o aplicativo Java foi baseado nos códigos de Jack Blitz do livro "Electrical and Magnetic Methods of Nondestructive Testing," segunda edição., editora Chapman and Hill.

https://rocarneval.neocities.org/EC_16-PlanImp.html

PÁGINA ANTERIOR https://rocarneval.neocities.org/EC_15-Pontes.html

PRÓXIMA PÁGINA https://rocarneval.neocities.org/EC_17-TelaMedidor.html

ÍNDICE https://rocarneval.neocities.org/EC_00-Indice(CP).html